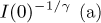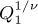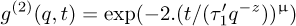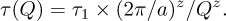| Issue |
Eur. Phys. J. Appl. Phys.
Volume 97, 2022
|
|
|---|---|---|
| Article Number | 25 | |
| Number of page(s) | 5 | |
| Section | Imaging, Microscopy and Spectroscopy | |
| DOI | https://doi.org/10.1051/epjap/2022210284 | |
| Published online | 01 June 2022 | |
https://doi.org/10.1051/epjap/2022210284
Regular Article
Modelling the statics and the dynamics of fluctuations in the ordering alloy AuAgZn2
1
Univ. Grenoble Alpes, CNRS, SIMAP,
38000
Grenoble,
France
2
Laboratoire d’Etude des Microstructures, UMR 104 CNRS-ONERA,
BP 72,
92322
Châtillon,
France
3
Laboratoire physique des materiaux, USTHB,
BP32 bab ezzouar
16111
Algiers,
Algeria
4
Center of the Physics of Materials, McGill University,
3600 University street,
Montreal,
PQ,
Canada,
H3A-2T8
* e-mail: frederic.livet@simap.grenoble-inp.fr
Received:
10
December
2021
Received in final form:
21
February
2022
Accepted:
22
February
2022
Published online: 1 June 2022
The ordering alloy AuAgZn2 has a Heusser second-order transition at Tc ≃ 336.4°C. Static measurements of the critical scattering were carried out at the BM02 beamline of the European Synchrotron Radiation Facility (ESRF). These results are compared with Monte-Carlo simulations of the Ising model and show that the model with a simple interaction between two neighbouring atoms of the simple cubic Au/Ag lattice fully explains the X-ray diffuse scattering. Dynamic measurements obtained from X-ray scattering below Tc and the observation of X-ray photon correlations at the ESRF ID10 beamline are compared with dynamic simulations. It is shown that this system follows the predictions of “model A” [P.C. Hohenberg, B.I. Halperin, Rev. Mod. Phys. 49, 436 (1977)] for a transition with non-conserved order parameter. The dynamics of ordering with nearest neighbour exchange of atoms in the simple cubic lattice is shown to be equivalent to the usual Ising spin flip model, but with a different time scale. A comparison between the kinetics of ordering and the dynamics of the observed speckles arising from critical fluctuations shows some discrepancy suggesting the need for further experiments.
© F. Livet et al., Published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
1 Introduction
The AuAgZn2 alloy exhibits a second-order ordering transition of the Heussler type [1]. The Au and Ag atoms occupy a simple cubic lattice, and the Zn atoms are in the center of this lattice. The High temperature phase with disordered Au and Ag atoms is called a B2 structure, and the ordered structure is the L21 structure (see Ref. [2]). From 15% to 35% atomic Au concentration, with the Zn concentration fixed to 50% [3], the B2 structure is stable until it melts. For this reason, the Zn atoms can be assumed fixed and one can focus on the Au/Ag ordering from a simple cubic (SC) structure to a face centered cubic structure (FCC) with double a lattice parameter. This tansition occurs close to Tc ≃ 336°C (609 K).
In this system, the order parameter is the difference in Au and Ag occupation of each cubic site, and ordering occurs by alternate occupation of neighbouring sites. The study of the static critical scattering above Tc shows this system belongs to the universal class of the 3-dimensional criticality with a one dimension order parameter [4] (see Ref. [5]). Writing the normalized temperature ϵ = |T — Tc|/Tc and the scattering vector of the Bragg superstructure peak 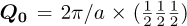 , where a = 3.17 A is the cubic lattice parameter of the high temperature disordered phase, the distance of a reciprocal lattice vector to Q0 is defined as Q.
, where a = 3.17 A is the cubic lattice parameter of the high temperature disordered phase, the distance of a reciprocal lattice vector to Q0 is defined as Q.
In systems like this alloy, ordering occurs in a simple cubic lattice with an antiferromagnetic Hamiltonian (AF). The statistics of the AF Ising model on a simple cubic lattice can be shown equivalent to the ferromagnetic Ising model, with a reversal of the sign of the nearest-neighbour interaction. The probability of a given configuration is identical to ferromagnetic Ising provided that the sign of nearest neighbour spins are reversed.
This means that the critical reduced Ising coupling ß has the same critical value: ßc = 0.22165459(4) [6–8]. In reciprocal space, fluctuations in a ferromagnetic system are observed in the small angle region. In an AF cubic system, the scattering is shifted by a vector Q0. The static properties of the alloy studied can thus be modelled with a classical ferromagnetic Ising model, which exhibits the same state probability.
In this system, the elementary dynamic process can be modeled by an exchange of two neighbouring Au/Ag atoms. This locally reverses the order parameter, and no long range atom migration is involved in the change of order. In a spin model, this local change is equivalent to a local change of the spin sign. This dynamics where the order parameter is not conserved is called the “model A” in references [9,10]. In this type of system, in the vicinity of Tc, a slowing-down of the fluctuations is connected to the large extension of the fluctuations. This model does not involve atom migration across the sample. It is adverse to “model B” (unmixing), where atoms have to diffuse across the lattice for the development of large scale fluctuations.
For dynamic simulations modelling of a spin system, like in reference [6], the elementary microscopic process is a single spin flip. In an ordering system, like the AuAgZn2 alloy studied here, the simple spin flip process is replaced by an exchange between Au or Ag nearsest-neighbours.
The aim of this paper is to make a detailed comparison of the statics and the dynamics of this transition between experiments carried out at the ESRF [1,5,11] and the simulations from the Ising model.
Firstly, the extension of the static fluctuations is studied. Then, from a comparison of simulated and measured ordering dynamics under Tc, a microscopic jump time is obtained in both simulations and experiments. This provides a dynamic calibration, and the dynamics of the fluctuations observed in an XPCS measurement are compared with simulations.
In the simulations, the lattice parameter is unity, and the corresponding reciprocal lattice position is written q. For comparison, Q = q x (2.π/a), and with this notation the q used in simulations can be thought as “hkl units” [6]. In this paper, the static and the dynamical experimental results obtained in the ordering transition are compared to Monte-Carlo (MC) simulations. In order to carry out this comparison, all experimental results are normalized to hkl units. In this paper, static simulations were done on a finite sized lattice with a L = 512 and an L = 1024 lattice was used for the dynamic simulations.
In the MC simulations, the static critical scattering is normalized 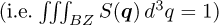 and the static scaling law characterizes the Ising system [5,12]:
and the static scaling law characterizes the Ising system [5,12]:
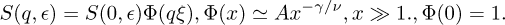 (1)
(1)
In equation (1), the fluctuation length ξ is an essential parameter, and γ ≃ 1.241 and v ≃ 0.631 [5]. In critical systems, ξ and S(q, ϵ) obey power laws:
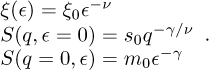 (2)
(2)
The power laws in equation (2) are universal, but the constants  and m0 are specific to the system studied. These constants can be obtained from MC simulations. For experimental results, the measured intensities I are given in photons per pixel per hundred seconds and S must be replaced by I in equation (2).
and m0 are specific to the system studied. These constants can be obtained from MC simulations. For experimental results, the measured intensities I are given in photons per pixel per hundred seconds and S must be replaced by I in equation (2).
The ordering kinetics was studied by quenching the alloy to temperatures close to Tc. The ordered domain sizes were obtained from measurements of the half width at half maximum (HWHM) of the superstructure peak. This estimate has the advantage of having a limited dependence on the detailed shape of the diffraction curve. By a simple fit to a Gaussian to the low Q part of the scattering curve, the HWHM Q1 is obtained. The domain size increase of the Ising model with a non-conserved order parameter is driven by the reduction of surface energy and can be written as:
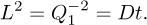 (3)
(3)
At T = 334°C, this value is [1] D334 = 4.9 x 105Å–2/s. Using 1.7eV for the activation energy [5], D336 = 4.4 x 105Å–2/s. This equation can be rewritten in a normalized form:
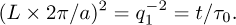 (4)
(4)
In this equation, the length is written in “hkl” units and a characteristic microscopic time is introduced:  . Here:
. Here: 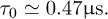
Close to the critical point, the dynamics of the fluctuations has been studied from the time-dependent intensity I(Q,t) in a coherent diffraction experiment by “X- ray photon correlation spectroscopy (XPCS)” [11]). The time-correlation of this intensity can be written:
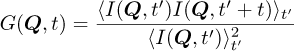 (5)
(5)
and this normalized correlation, after angular averaging, is written:
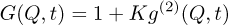 (6)
(6)
where K is the speckle contrast. If the scattered amplitude A(Q) of a system with a large number of atoms N is Gaussian distributed, g(2) can be written (“Siegert relation”) [6]:
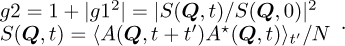 (7)
(7)
2 Observation and simulation of static fluctuations
A precise measurement of the static fluctuations was carried out at the D2AM beamline of ESRF. Figure 1 shows a typical measurement in the very vicinity of Tc. The detector was a 576 x 118 pixel detector with a 130 µm pixel size [13]. The sample was in vacuum and the sample to detector distance was 0.9 m. A vacuum flight path was used to reduce parasitic background. The measured temperature stability was better than 0.002 K. The horizontal Qperp direction corresponds to the direction perpendicular to the scattering vector Q0 In this figure, the intensities were carefully corrected for detector distorsion and a few cosmic rays. Intensity units correspond to counts per 100 s. Black dots correspond to discarded pixels (dead, blemished or cosmic rays). Apart from a central peak, connected to surface pretransitional scattering [11], the intensity is isotropic, as predicted for the fluctuations in this system. In this setup, Tc was shifted ≈ 2°C because of the separation between the measuring thermocouple and the diffraction spot.
A |Q|-average is carried out in an angular domain ±60° around the Q⊥ direction. This average is plotted in Figure 2a, in log scales. The pixel detector used is linear for intensities up to a few 105 ph/s.
Measurements were fitted by means of the equation:
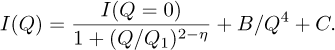 (8)
(8)
Equation (8) assumes that A ≃ 1. in equation (1). It was checked that the fast increase of the intensity for Q < 0.007Å–1 was 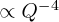 and that the main part of the curve of Figure 2a is critical scattering. This is checked in Figure 2b which shows the
and that the main part of the curve of Figure 2a is critical scattering. This is checked in Figure 2b which shows the 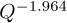 behaviour for
behaviour for 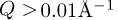 of the scattering, with a constant C ≃ 1.516(22) subtracted in all results above Tc. From fits at various temperatures above Tc, estimates of I(0), Q1 and of the critical exponent
of the scattering, with a constant C ≃ 1.516(22) subtracted in all results above Tc. From fits at various temperatures above Tc, estimates of I(0), Q1 and of the critical exponent 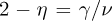 are obtained. From temperature linear fits of
are obtained. From temperature linear fits of 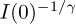 and
and 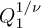 the critical temperature (in this experiment) can be precisely estimated. This is shown in Figure 3, where the linear fits yield estimates of Tc = 338.43(2). In Figure 3, the rounding of the transition can be observed. This means that equation (8) is not valid in a narrow range close to Tc. The largest value of
the critical temperature (in this experiment) can be precisely estimated. This is shown in Figure 3, where the linear fits yield estimates of Tc = 338.43(2). In Figure 3, the rounding of the transition can be observed. This means that equation (8) is not valid in a narrow range close to Tc. The largest value of 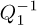 and I(0) observed at 338.6°C are
and I(0) observed at 338.6°C are 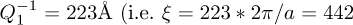 in dimensionless q-units) with a diffuse intensity of 9300 ph per 100 s per pixel).
in dimensionless q-units) with a diffuse intensity of 9300 ph per 100 s per pixel).
For each of the temperatures above Tc, equation (8) provides an estimate of 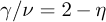 , and the results, plotted in Figure 4, yield 2 — ŋ = 1.9636(16), in agreement with reference [6]. In Figure 3, the linear fits correspond to:
, and the results, plotted in Figure 4, yield 2 — ŋ = 1.9636(16), in agreement with reference [6]. In Figure 3, the linear fits correspond to:  and
and 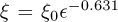 . In the dimensionless units of equation (2),
. In the dimensionless units of equation (2), 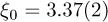 .
.
The experimental value of 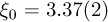 in equation (8) can be compared with the results of MC simulations in the vicinity of
in equation (8) can be compared with the results of MC simulations in the vicinity of 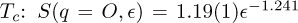 and
and 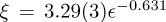 . These simulations were done in a L = 512 lattice, much larger that ξ. Both values of ξ0 agree well. This means that the q-variations of the measured fluctuations can be modelled with an Ising first- neighbour interaction, and that this ordering transition is well explained if Zn atoms are assumed fixed.
. These simulations were done in a L = 512 lattice, much larger that ξ. Both values of ξ0 agree well. This means that the q-variations of the measured fluctuations can be modelled with an Ising first- neighbour interaction, and that this ordering transition is well explained if Zn atoms are assumed fixed.
 |
Fig. 1 Static intensity observed around Q@ at 338.5° (here ≃ Tc + 0.07 K). Units are counts per 100 s per pixel. |
 |
Fig. 2 (a) Plot of the observed intensity after circular averaging of the pattern of Figure 1. The fit to equation (8) is shown (red line) (b) same plot after subtacting 1.5 and rescaling by Q1.964, demonstrating the critical scattering. |
 |
Fig. 3 Estimates of Tc. Linear behaviour of HT |
 |
Fig. 4 Various estimates of 2 – ŋ from fluctuating intensities above Tc. |
3 Kinetics of domain ordering
The kinetics of ordering was measured experimentaly and the time evolution of the size of the domains is described by equation (4).
The classical Monte-Carlo method for the simulation of the Ising model used in reference [6] was to randomly select a spin and to flip it according to a microcanoni- cal probability. The Glauber [14] probability was used in order to carry out time simulations [6]. As the present paper deals with an ordering alloy, the elementary atomic process is now an exchange between atoms on neighbouring sites. Each site and its neighbour (among 6) were randomly chosen.
Kinetic simulations were carried out in a lattice of longitudinal size 1024, and the unit time is MCS, which here corresponds to 230 elementary visits of pairs of neigbour- ing sites in the lattice. The intensity is obtained from the Fourier transform of the simulated lattice and a spherical average is carried out for intervals of  . Figure 5 shows the time evolution of S(q) for ß = 0.22387, i.e. 0.99 Tc. The system was quenched from complete disorder (i.e. S (q) = 1), and the irreversible ordering process was observed for t < 1000 MCS. Intensities are discarded for |q| > 0.25, and equation (8) is used to estimate the contribution of the fluctuations to the intensity. Åfter substracting these fluctuations, a Gaussian approximation was used for estimates of the HWHM q1.
. Figure 5 shows the time evolution of S(q) for ß = 0.22387, i.e. 0.99 Tc. The system was quenched from complete disorder (i.e. S (q) = 1), and the irreversible ordering process was observed for t < 1000 MCS. Intensities are discarded for |q| > 0.25, and equation (8) is used to estimate the contribution of the fluctuations to the intensity. Åfter substracting these fluctuations, a Gaussian approximation was used for estimates of the HWHM q1.
Values of 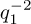 vs t (in MCS) are plotted in Figure 6 for T = 0.99 Tc. Classical behaviour is observed, except for short times, where the two terms of the scattering are difficult to distinguish.
vs t (in MCS) are plotted in Figure 6 for T = 0.99 Tc. Classical behaviour is observed, except for short times, where the two terms of the scattering are difficult to distinguish.
This method was used for five different temperatures. Table 1 summarizes the results normalized as in equation (4):
The resulting values of the microscopic times 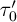 in Table 1 do not exhibit any significant temperature variation. The observed variations are essentially connected to the non- ergodicity in the dynamics of domain growth. These results can be significantly improved using a large number of quenches and averaging. Here, the value
in Table 1 do not exhibit any significant temperature variation. The observed variations are essentially connected to the non- ergodicity in the dynamics of domain growth. These results can be significantly improved using a large number of quenches and averaging. Here, the value 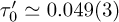 will be assumed.
will be assumed.
These estimates of the microscopic diffusion times, 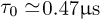 and
and  MCS provide the ratio
MCS provide the ratio 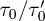 which connects MC simulations and experimental results in the AuAgZn2 alloy.
which connects MC simulations and experimental results in the AuAgZn2 alloy.
 |
Fig. 5 Time evolution of the intensity after a simulated quench to 0.99 Tc. |
 |
Fig. 6 The linear variation of the square of the domain size at 0.99Tc. |
Results of MC kinetics at various temperatures under Tc.
4 Dynamics of the fluctuations
The MC simulation of fluctuations involves the calculation of the function g(2)(|q|,t) at long time and |q| averaging. This method was discussed in reference [6]. A typical result is summarized in Figure 7 for a limited range of |q| and t values. Here, as for the study of domain growth, the atom nearest neighbour exchanges are studied, and the time scale is different than in reference [6], but results with a 1024 lattice size were fitted with the same equation:
here z = 2.017 and 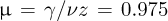 . From fits in a q range 0.013 < q < 0.033 and a t(MCS) range 0.5 < t < 400, one obtains
. From fits in a q range 0.013 < q < 0.033 and a t(MCS) range 0.5 < t < 400, one obtains 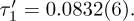
Writing for the speckle fluctuation in the AuAgZn2 alloy the same equation (10) with an elementary time T1, the result is:
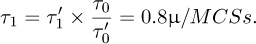 (11)
(11)
This value of T1 transforms the MCS in the simulations to microseconds in the experiment. It is used for a comparison with the dynamic measurement of the fluctuations in the AuAgZn2 system. Results from the ID10 beamline of ESRF [11] are plotted in Figure 8. The black line in this figure shows the present estimate of t(Q) at Tc in equation (10) with:
There is a clear contradiction between the results of the dynamic simulations (black line) and the observed fluctuation time (t(Q, T)) for temperatures close to Tc, estimated as 336.012°C in this experiment. The origin of this discrepancy is probably in an erroneous interpretation of the measured data. In this experiment, the correlation function was written by means of equation (6), where XPCS is assumed homodyne. In the case of the alloy studied, a large pre-transitional diffuse scattering is observed. In our previous paper, interferences between the amplitude of this diffusion and that of fluctuations were neglected. If an amplitude mixing is assumed, the scattering can essentially be written [15,16]:
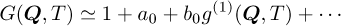 (13)
(13)
and 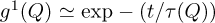 If heterodyning is assumed, the observed time from XPCS t(Q) is doubled. The corresponding result is plotted in Figure 8 (dashed black line), and it fits remarquably well to the XPCS results.
If heterodyning is assumed, the observed time from XPCS t(Q) is doubled. The corresponding result is plotted in Figure 8 (dashed black line), and it fits remarquably well to the XPCS results.
 |
Fig. 7 A representation of the function g(2) at the critical temperature, from a series of 1000 MCS. |
 |
Fig. 8 Comparing the results of reference [11] with the simulations: the black line corresponds to simulating the results with the homodybe hypothesis and the black dotted line with the heterodyning hypothesis. |
5 Discussion
The static fluctuations of the AuAgZn2 alloy are well modelled by a simple Ising model. The ordering kinetics and the dynamic fluctuations have been studied in this paper. Table 2 summarizes the various results obtained.
In Table 2, the experimental results of the measured static intensities are well explained with the Ising model: after a calibration between measured intensities and modelled S(q, ϵ), the results are identical which means that the system has a nearest neghbour interaction range (identical ξ0).
A clear connection can be established between the dynamics of the simulations and the measured dynamics, provided that heterodyning is assumed. Though the elementary atom jump time is of the order of the microsecond, the collective dynamics is in the range of seconds, which corresponds to large critical slowing-down. The experimental results in the measurements of the dynamics at the ESRF are too imprecise to carry out statistical tests to verify the heterodyne asumption, as they are unprecise in the determination of the dynamic exponent z. Better studies require a more coherent and more intense beam such as can now be obtained at the new Extremely Brilliant Source (EBS) of the ESRF [17].
Summary of results: m0, ξ0 and s0 are defined in equation (2), “A” in equation (1), T0 in equation (4) and T1 in equation (10).
Author contribution statement
All the authors were involved in the preparation of the manuscript. All the authors have read and approved the final manuscript.
References
- F. Livet, M. Fèvre, G. Beutier, M. Sutton, Phys. Rev. B 92, 094102 (2015) [CrossRef] [Google Scholar]
- F. Reynaud, Phys. Status Solidi A 72, 11 (1982) [CrossRef] [Google Scholar]
- M.E. Brooks, R.W. Smith, Scripta Met. 3, 667 (1969) [CrossRef] [Google Scholar]
- J. Zinn-Justin, Phys. Rep. 344, 159 (2001) [CrossRef] [MathSciNet] [Google Scholar]
- F. Livet, F. Bley, J.P. Simon, R. Caudron, J. Mainville, M. Sutton, Phys. Rev. B 66, 134108 (2002) [CrossRef] [Google Scholar]
- F. Livet, Phys. Rev. E 101, 022131 (2020) [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- P. Hou, S. Fang, J. Wang, H. Hu, Y. Deng, Phys. Rev. E 99, 042150 (2019) [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- A.M. Ferrenberg, J. Xu, D.P. Landau, Phys. Rev. E 97, 043301 (2018) [CrossRef] [PubMed] [Google Scholar]
- B.I. Halperin, P.C. Hohenberg, Phys. Rev. 177, 952 (1969) [CrossRef] [Google Scholar]
- P.C. Hohenberg, B.I. Halperin, Rev. Mod. Phys. 49, 436 (1977) [Google Scholar]
- F. Livet, M. Fevre, G. Beutier, F. Zontone, Y. Chushkin, M. Sutton, Phys. Rev. B 98, 014202 (2018) [CrossRef] [Google Scholar]
- J.C.L. Guillou, J. Zinn-Justin, J. Phys. 48, 19 (1987) [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- P. Pangauda, S. Basolo, N. Boudet, J.F. Berar, B. Chantepie, J.C. Clemens, P. Delpierre, B. Dinkespiler, K. Medjoubi, S. Hustache et al., Nucl. Instrum. Methods Phys. Res., Sect. A 591, 159 (2008) [CrossRef] [Google Scholar]
- R. Glauber, J. Math. Phys. 4, 294 (1963) [CrossRef] [Google Scholar]
- C. Gutt, T. Ghaderi, A. Madsen, T. Seydel, M. Tolan, M. Sprung, G. Grübel, S.K. Sinha, Phys. Rev. Lett. 91, 076104 (2003) [CrossRef] [PubMed] [Google Scholar]
- F. Livet, F. Bley, I. Morfin, F. Ehrburger-Dolle, E. Geissler, M. Sutton, J. Synchrotron Rad. 13, 453 (2006) [CrossRef] [PubMed] [Google Scholar]
- P. Raimondi, Synchrotron Radiat. News 29, 8 (2016) [CrossRef] [Google Scholar]
Cite this article as: Frédéric Livet, Mathieu Fèvre, Guillaume Beutier, Fadi Abouhilou, Mark Sutton, Modelling the statics and the dynamics of fluctuations in the ordering alloy AuAgZn2, Eur. Phys. J. Appl. Phys. 97, 25 (2022)
All Tables
Summary of results: m0, ξ0 and s0 are defined in equation (2), “A” in equation (1), T0 in equation (4) and T1 in equation (10).
All Figures
 |
Fig. 1 Static intensity observed around Q@ at 338.5° (here ≃ Tc + 0.07 K). Units are counts per 100 s per pixel. |
| In the text | |
 |
Fig. 2 (a) Plot of the observed intensity after circular averaging of the pattern of Figure 1. The fit to equation (8) is shown (red line) (b) same plot after subtacting 1.5 and rescaling by Q1.964, demonstrating the critical scattering. |
| In the text | |
 |
Fig. 3 Estimates of Tc. Linear behaviour of HT |
| In the text | |
 |
Fig. 4 Various estimates of 2 – ŋ from fluctuating intensities above Tc. |
| In the text | |
 |
Fig. 5 Time evolution of the intensity after a simulated quench to 0.99 Tc. |
| In the text | |
 |
Fig. 6 The linear variation of the square of the domain size at 0.99Tc. |
| In the text | |
 |
Fig. 7 A representation of the function g(2) at the critical temperature, from a series of 1000 MCS. |
| In the text | |
 |
Fig. 8 Comparing the results of reference [11] with the simulations: the black line corresponds to simulating the results with the homodybe hypothesis and the black dotted line with the heterodyning hypothesis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.