| Issue |
Eur. Phys. J. Appl. Phys.
Volume 93, Number 1, January 2021
|
|
|---|---|---|
| Article Number | 10901 | |
| Number of page(s) | 14 | |
| Section | Physics of Energy Transfer, Conversion and Storage | |
| DOI | https://doi.org/10.1051/epjap/2020200187 | |
| Published online | 06 January 2021 | |
https://doi.org/10.1051/epjap/2020200187
Regular Article
A novel ANN-based method for simultaneous estimation of thermophysical properties using experimental photothermal data
1
Processes, Materials and Solar Energy (PROMES-CNRS, UPR 8521), Tecnosud, Rambla de la Thermodynamique, Perpignan 66100, France
2
Processes, Materials and Solar Energy (PROMES-CNRS, UPR 8521), 7 rue du Four Solaire, Font-Romeu-Odeillo-Via 66120, France
3
University of Perpignan Via Domitia, 52 Avenue Paul Alduy, Perpignan 66860, France
* e-mail: reine.reoyo@promes.cnrs.fr
Received:
17
June
2020
Received in final form:
14
October
2020
Accepted:
13
November
2020
Published online: 6 January 2021
In this paper, a novel artificial neural network (ANN) based method dedicated to simultaneously estimating thermal conductivity and thermal diffusivity of CSP (concentrating solar power) plant receiver materials is presented. By monitoring the evolution of these two correlated thermophysical properties during aging cycles, CSP plants' cost efficiency could be maintained. The proposed method is based on the processing of experimental photothermal data using classification and estimation networks. All the networks are feedforward ANN trained with supervised learning algorithms. A pseudo random binary signal (PRBS) is used as excitation and the impact on performance of both the photothermal response length, which is used as model input, and the number of training examples has been evaluated. Of course, the networks' topology has been optimized, allowing the generalization ability to be controlled. Despite the lack of data, the results are promising. Mean relative errors are between 8% and 20%, and the main levers for improvement are identified. In this paper, the study deals with a large range of materials (polymers and metallic alloys).
© R. Reoyo-Prats et al., EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Thermophysical characterization of materials is an issue in various domains such as building design (for estimating the insulating performance of a given structure) or energy plant optimization. In concentrated solar power plants, the monitoring of thermophysical properties enables to notice the degradation of solar receivers. Indeed, the materials are submitted to strong climate conditions and maintaining the thermophysical properties is a key issue to ensure cost-efficiency of CSP plants: thermal conductivity is about the ability of a given material to transfer heat by conduction during a stationary phase, as a sunny day, whereas thermal diffusivity is about the ability of this material to respond to a sudden temperature change, for example caused by a cloudy day.
Depending on the property to be estimated, the kind of material to be characterized (polymers, metals, etc.) and the available sample shape, a well-known method can be used. Regardless of the method, an appropriate physical model is needed.
The methods involving steady-state experiments are used to estimate thermal conductivity (λ), which is expressed in W m−1 K−1, or contact thermal resistance (R), which is expressed in m2 K W−1. The guarded hot plate method [1–3] is a standardized one (ISO 8301:1991, ISO 8302:1991). A controlled heat flux is applied on one side of the sample. On the other side, temperature stays constant thanks to a thermostatically-controlled water bath. The difference in temperature between the two sides of the sample is measured and thanks to the Fourier's law is used to determine thermal conductivity. This method is operable for insulating materials, since contact thermal resistance is negligible with respect to the sample resistance. The same method, based on Fourier's law, is used for conductive materials with a different device: a stepped bar apparatus [4,5]. In this case, the sample has a pipe form, and temperature is measured using several thermocouples positioned on the tube. In this configuration, lateral thermal losses are not negligible, and have to be considered in the model. This method is difficult to accurately set up because controlling the convective heat transfer coefficient is necessary.
Methods involving unsteady-state experiments exist. The hot wire standardized technique (standard ISO 8894) [6] and the hot disk method, or transient plane source [7,8], use an electrical resistance (in the wire or in the hot disk) which is positioned between two samples. The heating device is also used to measure changes in temperature during the heating phase. Then, the thermal conductivity is deduced from an adequate physical model. The photothermal experiment is another option among the unsteady-state experiments, which is commonly used for thermophysical properties estimation. The flash method consists in a short pulse hitting a sample on its front face. Changes in temperature are recorded on the front-face surface or the rear-face surface. Then, measurements can be compared to estimations given by a physical model. Thermal diffusivity (a), which is expressed in m2 s−1, and specific heat capacity (Cp), which is expressed in J kg−1 K−1, can be estimated by identification. This laser flash experiment has been developed by Parker et al. [9] using the Carslaw and Jaegger model [10], a one-dimensional adiabatic model with a Dirac impulse used as excitation, that is, an infinite pulse of energy. The main issues are related to thermal losses and the excitation characteristics. The model has been improved since its first publication: the models developed by Cowan [11] and Clark and Taylor [12] can be used to consider convective or radiative losses. The Larson and Koyama model [13] can be used with a finite pulse excitation. Nowadays, this experiment is still commonly used thanks to standardized LFA (Laser Flash Apparatus) devices. The studies carried out by Min et al. [14], Pinto et al. [15] and Abdulagatov et al. [16] are linked to this experiment. Nevertheless, in order to estimate various properties simultaneously, like for example thermal diffusivity (a) and heat capacity (Cp), another experiment, often DSC (Differential Scanning Calorimetry) must be carried out to determine heat capacity. Moreover, in case of some differences between the model and the experimental conditions, properties identification gets more complicated and less accurate. Lastly, when estimating thermal conductivity (λ) using this method, it is necessary to calculate it thanks to the previous estimation, knowing the density ρ (kg m−3), so the error committed for the estimation of thermal diffusivity is propagated (see Eq. (1)).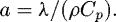 (1)
(1)
In combination with the impulse photothermal experiment, an inverse method based on an adequate physical model can be used [17]. As another interesting work, Pavlov et al. [18] have proposed a method to estimate thermal conductivity, specific heat capacity or total hemispherical emissivity by taking into account the radial distribution of the considered property. Step by step, the property is estimated in the center of the sample and stored, then the neighboring values are gradually estimated up to the edge. Nevertheless, using this method, both thermal diffusivity and thermal conductivity cannot be estimated simultaneously. Indeed, inverse methods are unable to estimate correlated values simultaneously since they proceed to the inversion of a sensibility matrix. Again, it is possible to deduce the second property from the first one but the error committed for the estimation of the first property is propagated to the second property. In order to overcome this limitation, Orain et al. [19] have used a genetic algorithm instead of a gradient-based algorithm for iteratively estimating the properties. This non-gradient method is considered as an evolutionary algorithm. It is advantageous since it involves, for each iteration, the generation and the test of a random population composed of a large number of individuals (vectors of possible properties). Thanks to selection, crossover, and mutation operations, which are iteratively repeated, the objective function is gradually minimized. Nevertheless, an adiabatic model is considered. So, it is crucial to minimize heat losses during the photothermal experiment. Moreover, the model can only be used if thermal effusivity is known. To have a relevant estimation of the effusivity, another experiment is needed.
As an interesting option, photothermal responses can be exploited using machine learning methods. These methods have several advantages. First, physical knowledge about experimental conditions is not required. So, difficulties related to the correspondence between the model and experimental heat losses or the finite pulse excitation can be overcome. Moreover, these methods are not constrained by correlated properties, since one can exploit non-physical parameters or the possibilities these methods offer when it comes to find an adequate topology. As a result, thermal conductivity and thermal diffusivity can be estimated simultaneously, avoiding error propagation. During the past few years, several studies have focused on the use of machine learning tools for thermophysical characterization of materials from photothermal responses [20–22]. In these papers thermal diffusivity and thermal conductivity are simultaneously estimated using side-by-side artificial neural networks or adaptive neuro-fuzzy inference systems (ANFIS). All the training examples come from simulated data. In this paper, a neural structure is proposed: feedforward ANN trained with supervised learning algorithms are used for classification and properties estimation. One model is developed for each of the classes, allowing both properties to be estimated simultaneously from experimental photothermal data. The neural structure is first developed with the purpose of being operable with a wide range of materials and behaviors. In a second phase, this tool will be adjusted to CSP absorber materials.
The paper is organized as follows: in Section 2, the neural structure based on feedforward artificial neural networks allowing thermal diffusivity and thermal conductivity to be simultaneously estimated for two classes of materials is presented. The database is composed of polymers and metallic alloys. The evaluation method is presented in Section 3. In Section 4, the training and validation examples obtained thanks to the photothermal experiment are presented and the results are analyzed. Section 5 concludes the paper and addresses future work.
2 Neural network structure
In this section, the neural structure designed for this study is presented. An artificial neural network (ANN) consists in a chain of mathematical operators connecting the chosen inputs to the desired outputs. In order to design an effective neural network for simultaneously estimating thermophysical properties, the determination of a correct topology is a key point: the inputs and outputs and the number of hidden layers and units (hereinafter referred to as hidden neurons) in each hidden layer (to be optimized by controlling the network's generalization ability).
In the present study, the objective is to estimate simultaneously the thermal diffusivity and thermal conductivity of a wide range of materials, using their thermal responses to a pseudo random binary signal. So, the only network's input is a sequence describing the evolution of temperature over time. In order to estimate the desired properties, two strategies are possible. The first one consists in developing a universal model capable of providing estimates of the two thermophysical properties of interest for all the materials, regardless of their behaviors. The second strategy consists in developing specific models, one for each class of materials (in the present case, polymers and metallic alloys) highlighted by the classification network. Usually, the first strategy leads to a less complex neural structure, with a reduced number of parameters to identify during the training phase, but less efficient than specific models. With the second strategy, the range of possible values for both properties is reduced. So, we have decided for the development of a classification tool and specific models.
The first point to consider is the samples' behavior: evolution of temperature for an insulating material will be sharper than the one of a conductive material (this will be detailed in Sect. 4.1.2). So, two classes seem to be recognizable. In order to deal with different kinds of responses, leading to different properties ranges, we created a preliminary neural network (Fig. 1). It is a feedforward neural network (FNN) designed for supervised classification, used to separate the available materials into two classes (the first class for materials with low diffusivity and low conductivity values, and the second class for materials with higher diffusivity and higher conductivity values). Then, an estimation feedforward neural network is designed for each class. Each neural network has two outputs: thermal diffusivity and thermal conductivity.
 |
Fig. 1 The neural structure. |
3 Evaluation method
Artificial Neural networks are highly sensitive to the initial values of the weights and biases which are randomly selected in a given interval. The final values of the weights and biases are given by the supervised training algorithm used, on the basis of an iterative calculation. So, the ANN parameters will be different for different sets of initial values of the weights and biases. In order to check the generalization ability of a trained network, several new examples are presented to it. This phase is known as the validation phase. From these examples, it is possible to calculate the mean relative error between the expected values and the output estimated values (i.e. the generalization error).
If the generalization error is similar for different neural models (coming from different initial weights and biases), the model is considered to be stable. If it is not the case, the network's topology can be modified. In order to check the network's stability, it is necessary to repeat the entire procedure (training and validation) several times (Fig. 2). We choose to reiterate it 50 times. After each training and validation phases, regardless of the results of the other tests, it is possible to determine if the obtained neural model is inconsistent. Indeed, both outputs (thermal diffusivity and thermal conductivity) must be positive. So, a model producing, at least, one negative value for one of the validation examples, is considered to be inconsistent. For the consistent neural models, the mean relative errors of thermal diffusivity and thermal conductivity are calculated. After 50 trials and after removing all the inconsistent models, we have calculated the first and third quartiles (Q1 and Q3) of both mean relative error series (for thermal diffusivity and thermal conductivity). We have used the interquartile range (IQR) of each series to determine the outlier values (ε
out, see Eq. (2)). (2)
(2)
When this procedure is over, two results are exploitable. First, the number of neural models providing inconsistent or outlier values allows to evaluate the network's stability and, secondly, the resulting global average error of thermal conductivity and thermal diffusivity allows to check the accuracy of the proposed estimation method.
 |
Fig. 2 Network stability – determination of the inconsistent networks and outlier values. |
4 Network development
The creation of a relevant database is a major challenge in the development of an efficient neural model for estimating. The test bench used for this work and some typical photothermal responses are presented in Section 4.1. The classification network is presented in Section 4.2 and both estimation networks are presented in Section 4.3.
4.1 Test bench and experimental examples
In this subsection, the experimental setup and the database made up of the thermophysical properties of 30 material samples are presented and an overview of some of the characteristics of the samples' responses is given.
4.1.1 Test bench settings
In order to develop a consistent neural model, we have decided for experimental photothermal data (for both the networks' training and validation phases). A photothermal test bench is set up (Fig. 3): a laser excites a sample thanks to a laser command connected to the computer. Then the radiance variation of the sample is detected by an infrared (IR) camera which measure the evolution of temperature on the materials' front face. The signal is recorded directly on the computer.
The laser is an Er-Yb diode laser of 3 W in collimated beam with a square cross section of 1.1 × 1.1 mm2, and a low divergence (4 mrad). The peak wavelength is between 970 and 980 nm. The asymmetric radiation from the laser diode is transformed into a symmetrical beam using a patented micro optics. It is controlled via the computer using the “UM DiTec” laser diode driver and temperature controller. Depending on the desired experiment, it is possible to decide for different excitation profiles (pulse, sinusoid, squared signal, periodic or not…), by controlling the frequency, voltage, and current. The laser hits the middle of the sample, situated at 50 cm, with a rise time and a fall time which are under 15 μm. We do not use any focusing lens, so the spot on the sample surface is approximately 5 mm diameter.
The photothermal experiment is often carried out with a continuous wave excitation or a pulsed excitation. For the first one, both the amplitude and phase of the signal are observed and the experiment has a very good signal to noise ratio but its analysis is quite slow since it is necessary to proceed to many experiments to have various frequencies. For the second one, the pulse response of the material is observed. The analysis is faster since the experiment provides multifrequency information. Nevertheless, the signal, as close as possible to a Dirac signal, implies the release of a big amount of energy in a short period of time. The pseudo random binary signal, − such a signal is used in various studies [23,24] − allows the possibility to work with a multifrequency response without the big thermal stress induced by a pulse excitation. In the present study, we have based our work on previous developments. First, we rebuilt the impulse responses of materials from their responses to a PRBS using artificial neural networks and used an inverse method to estimate thermal diffusivity [25]. In this study, it was demonstrated that rebuilding the impulse response was not required and, as a result, one can directly estimate thermophysical properties from responses to a PRBS using artificial neural networks. Then, two papers [20,21] focused on evaluating the performance of such an approach with a simulated experiment. In that case, the whole PRBS signal was used. Now, we highlight the possibility of shortening it in order to save experimental and computing time (see Fig. 4). The samples are excited with a 3V-5A laser signal.
The infrared camera FLIR A320 has a spectral sensitivity of 7.5–13 μm. It is used to detect and transmit the evolution of the sample temperature. It can be situated on the front face of the sample, or on its rear face. The temperature is registered with a non-constant frequency (approximately 4 measures per second). So, a linear interpolation is realized as a post-treatment to access to the temperature at each second.
In the present study, we measured the temperature in the middle of the front face of the sample. To limit the noise level, we consider the average temperature in a circle of radius equal to 7 mm.
 |
Fig. 3 Photothermal test bench at PROMES-CNRS. |
 |
Fig. 4 Beginning of the PRBS sequence used excitation profile. |
4.1.2 The samples and their photothermal responses
The examples dataset is made up of 30 photothermal responses associated with thermal diffusivity/thermal conductivity couples (Tab. 1). The set includes polymers such as PMMA (polymethyl methacrylate, sample n°6), metallic alloys such as Inconel 625® (sample n°23) and a ceramic sample, the boron nitride (sample n°30).
On one hand, we recovered data about all these samples. The objective is to know as accurately as possible the real properties of each sample in order to train the artificial neural networks properly, and to evaluate the results of the validation phase with accurate data. For this purpose, we took thermal diffusivity/thermal conductivity data from the manufacturer who provided us the samples, but these values were merely estimated. So, we compared these values with values coming from other manufacturers and from the literature (see Appendices). For each sample, we chose to work with mean value of both thermal diffusivity and thermal conductivity.
The dataset (Tab. 1) is divided in several subsets in order to test different data combinations for the training phase. Set 1 is composed of the samples in green (8 samples). In Set 2, the samples in blue are added (15 samples). In Set 3, the samples in purple are added (18 samples). In Set 4, the samples in orange are added (22 samples). The samples in pink are used for validation (7 samples). The sample 20 is quartz. Because it is transparent, the laser excitation goes mainly through the material, and the signal recorded by the infrared camera in front of the sample is not significant. Therefore, this sample is not added to the previous sets.
On another hand, we proceeded with the experimental phase. The samples are circular with a diameter of 25, 40 or 50 mm (depending on the manufacturer available sizes) and their thickness is 8 mm. For each sample, the photothermal experiment is realized in the same conditions (see Sect. 4.1.1). Some examples of the normalized responses are presented in Figure 5. The normalization is done thanks to the highest value in the considered sequence. This data treatment allows neglecting the optical properties of the samples, so we can only consider the thermophysical properties.
Examples distribution depending on their thermal conductivity and diffusivity.
 |
Fig. 5 Examples of photothermal responses. |
4.2 Development and test of the classification network
In this subsection, we present the first part of the neural structure: the classification network.
4.2.1 Structure of the classification network
We used a feedforward artificial neural network trained with a supervised learning algorithm to develop the classification algorithm, with two apparent classes. Unlike the simulated database used in previous work [21], we observe in Table 1 that the real materials available do not cover all the possible combinations for the thermal diffusivity/thermal conductivity couple. The higher the thermal conductivity, the higher the thermal diffusivity, and vice versa. A material with high-low or low-high values of both properties does not have a physical existence. So, we highlight a class of materials with low thermal conductivity and low thermal diffusivity (these materials are polymers, i.e. the samples 1–19 in Tab. 1) and a class of materials with higher values of both properties (these materials are metallic alloys and ceramics, i.e. the samples 21–30 in Tab. 1). In total, 22 samples are used for the training phase (15 samples from Class 1, 7 samples from Class 2), and 7 samples for the validation phase (4 samples from Class 1, and 3 samples from Class 2). The classification seems obvious with this example set. But the network is designed to be able to deal with some unknown samples or materials for which the affiliation to the first or second class is more complicated. For each sample, the network input is its photothermal response normalized to its highest value in the considered sequence. The impact on performance of the photothermal response length has been studied, considering 5 to 100 s responses.
Regarding the network's topology, it consists in 2 layers. A single hidden layer is considered. Each unit in the layer uses a hyperbolic tangent function as activation function, defined as follows: S(z) = sinh(z)/cosh(z). The impact of the number of hidden neurons on the network's generalization ability has been evaluated. The output layer contains two units (one for thermal diffusivity and one for thermal conductivity) and uses the softmax function as activation function (see Eq. (3)). For each output, a value between 0 and 1 is obtained and the sum of outputs is equal to 1. So, these output values suggest the class to which the example belongs, that is, Class 1 or Class 2. (3)
(3)
with: j, number of the class, 1 or 2; zj , the input j of the activation function for the class j; K the total number of classes, here 2.
For the training phase, the scaled conjugate gradient (SCG) algorithm is used. As all the conjugate gradient (CG) methods, this one uses the second derivative of the goal function, the Hessian matrix. Instead of considering only the gradient descent direction, the CG algorithms take a direction which is conjugate to the directions of the previous steps. Moreover, the SCG algorithm uses a scalar to regulate the Hessian matrix.
4.2.2 Classification network: results and discussion
Both the efficiency and stability of the classification network presented above are evaluated. After completing the training and validation phases, we check if the network performs well when it comes to correctly classify all the validation examples (7 samples). This reflects the network's efficiency. Because artificial neural networks are highly sensitive to the initial values of the weights and biases, which are updated during the training phase, we repeated the process 50 times and counted how many times the network performs a complete success. This is what we call in the sequel “network's stability”, summarized in Table 2. The “complete success” rate is evaluated for several photothermal response lengths, different number of hidden neurons, and the 4 example sets available.
First, we observe that using Set 1, most of the time the classification network does not perform well. Set 1 has only 8 training examples, for 7 validation examples. Usually, artificial neural networks need a large set of training examples, providing exhaustive information, to learn properly. Set 1 seems to be composed of a too low number of training examples. Nevertheless, depending on both the photothermal response length and the number of hidden neurons, the training process can be efficient enough to properly classify the validation examples. It is the case for a photothermal response length of approximately 30 s, or above 60 s.
On one hand, we observe for all the sample sets that the most critical factor is not the number of hidden neurons but the photothermal response length. Below 10 s, regardless of the set or the number of hidden neurons, it appears that, in that case, the information the photothermal responses provide is incomplete and, as a result, not relevant enough. On the other hand, when using Set 3 and Set 4, we observe that for a photothermal response length of 65 and 75 s, respectively, performance decreases again. This can be due to a sort of redundancy or a similarity in the normalized sample responses for a time span.
Stability of the classification network depending on the photothermal response length and the number of hidden neurons, for the 4 example sets.
4.3 Development and test of the feedforward networks for properties estimation
In this subsection, we present the second part of the neural structure: the feedforward neural networks used to simultaneously estimate thermal diffusivity and thermal conductivity for both classes.
4.3.1 Structure of the feedforward networks
We have developed two estimation models based on feedforward neural networks trained with a supervised learning algorithm, one for each class (Class 1 is composed of samples 1–19, i.e. low thermal conductivity and low thermal diffusivity materials, and Class 2 is composed of samples 21–30, i.e. higher thermal conductivity and thermal diffusivity materials). For both networks, the temperature evolution normalized to the highest temperature observed among all samples in the considered sequence is used as input. As for the classification network, inputs are studied: the same sets, split by classes, are tested (Class 1 examples are tested in first neural network, Class 2 examples in second neural network), and the impact of photothermal response length is investigated.
Regarding the training phase, we have used for both networks the well-known Levenberg-Marquardt (LM) algorithm. It is a robust algorithm which uses an approximation of the Hessian matrix using the Jacobian matrix. Thanks to an adaptive learning rate, LM method combines classical gradient method and Gauss-Newton algorithm. Some other training algorithms such as the gradient descent, Bayesian regulation, or conjugate gradient have been tested unsuccessfully: performance was lower and/or the number of required iterations significantly higher.
The topology consists in a single hidden layer with units − the number of hidden units has to be optimized − using non-linear sigmoid-shape activation functions and an output layer with two units using linear activation functions (one unit per thermophysical property).
4.3.2 Results and discussion
As previously stated in the paper, the feedforward neural networks used are tested by varying some factors: the set of examples, the photothermal response length and the number of hidden neurons. For each test, we use the evaluation method described in Figure 2. The figures below show how the estimates are accurate. The generalization error is presented. 50 iterations are performed during training.
4.3.2.1 Example sets
First, the models are developed, for each class, by using the same network, composed of one hidden layer of 20 neurons. The considered photothermal responses are 40 s length. Such a duration is chosen as a compromise, based on experience, between a too short response which would provide insufficient information to the networks and a too long response which could lead to the introduction of redundant information. In both cases, generalization ability can be negatively impacted. In the following step, after having chosen the best example set, the photothermal response length is adjusted. Let us examine both classes. Indeed, we presented in Sections 4.1.2. and 4.2.1. the differences between the training sets: for Class 1, we progressively add some new training examples at each new set (4, 8, 11 and 15 for sets 1, 2, 3 and 4, respectively); for Class 2, due to the low number of available examples, we just add some new examples at set 2 (7 training examples for 3 validation examples).
For Class 1, we observe that performance is globally higher when adding some examples to the training set, until Set 3. For thermal diffusivity, the mean relative errors are 19.8%, 14% and 9.3% for Set 1, Set 2, and Set 3, respectively. When adding some new examples to Set 4, the error raises to 14.7%. This probably means that the examples added to Set 4 do not provide useful information to the network. The highest thermal conductivity error is obtained for Set 1 (28.2%). Then, performance is similar with Set 2, Set 3 and Set 4: 18.3%, 19.8% and 16.7%, respectively.
For Class 2, we notice that the number of examples in Set 1 is not enough for both thermophysical properties to be estimated correctly. Using Set 1 leads to the highest thermal conductivity error, that is, 27%, whereas it is 17.6% with Set 2. For thermal diffusivity, the results are similar with both sets (Fig. 6).
 |
Fig. 6 Impact on performance of the example sets. Left: Class 1. Right: Class 2. |
4.3.2.2 Photothermal response length
Using Set 3 for Class 1 (11 training examples and 4 validation examples) and Set 2 for Class 2 (7 training examples and 3 validation examples) and considering 20 neurons in each hidden layer, we tested different photothermal response lengths (see Fig. 7). We observe that the mean relative error decreases sharply when the response length increases and reaches 30 s. Then, the error decreases slightly for responses whose lengths are between 30 and 50 s. After this point, the error is stable or slightly increasing.
 |
Fig. 7 Impact on performance of the photothermal response length. |
4.3.2.3 Number of hidden neurons
The impact on performance of the number of hidden neurons has been evaluated using Set 3 for Class 1 and Set 2 for Class 2 as well as a 50-s photothermal response. For both networks, we notice overfitting when too many neurons are added to the networks' hidden layers (see Fig. 8). For the Class 1 network (polymers), this phenomenon, which impacts generalization ability, is quite slight but noticeable for a number of hidden neurons higher than 60, approximately. For a lower number of hidden neurons, performance is stable with a mean relative error around 20%. For the Class 2 network, overfitting is clearly apparent for a number of hidden neurons higher than 15. Moreover, for a number of hidden neurons higher than 50, the network is not just less efficient, it is also unstable. Indeed, among the 50 networks we trained and validated, approximately 20% of these networks are considered inconsistent or provide outlier values.
For Class 1, the best performance is given by a network with 26 hidden neurons: the mean relative error is 8.7% for thermal diffusivity and 19.3% for thermal conductivity. For Class 2, the best performance is given by a network with 6 hidden neurons only: the mean relative error is 21.3% for thermal diffusivity and 18.7% for thermal conductivity.
 |
Fig. 8 Impact of the number of hidden neurons. |
4.4 Overall relative estimation error
In addition to the mean relative error, it is interesting to take a look at the relative estimation error for each material. Figure 9 shows the errors given by the selected model, for each class, instead of showing average errors among 50 trained and validated networks. In this figure, several pieces of information are entered. First, the values (given by manufacturers or taken from the literature) for thermal diffusivity and thermal conductivity used to develop the model are highlighted: the average value, but also the minimum and maximum values. Then, the estimated value given by the model is depicted. The highlighted error corresponds to the relative error between the average value from the literature and the estimated value given by the model.
We can observe that the error is very different from one material to another in the same class: for example, in Figure 9c (Class 2), the thermal conductivity of sample 26 is estimated with an error of 0.1% whereas the thermal conductivity of sample 28 is estimated with an error of 25%. Moreover, we observe that the values taken as references for the development of the model vary within a certain range, as shown by the properties' minimum and maximum values in the figure. For example, sample 8 (Fig. 9a) has a thermal conductivity between 0.22 and 0.37 W m−1 K−1. For this sample, the model gives an estimation of 0.20 W m−1 K−1, which represents an error of 31% when considering as reference the average value from the literature, and an error of only 9% when considering as reference the lowest value available. This means that the values considered as references may not be accurate enough and, as a result, penalize the neural network training. To deal with this issue, it would be suitable to correct the database with measured values of thermal conductivity and thermal diffusivity.
 |
Fig. 9 Estimation of properties and corresponding relative estimation errors for Class 1 and Class 2. |
5 Conclusion and outlook
A machine learning based method, resorting to feedforward artificial neural networks, is proposed for the estimation of two thermophysical properties: thermal diffusivity and thermal conductivity. Specific models are developed for two classes of materials. By monitoring the evolution of these properties during aging cycles, cost efficiency of concentrated solar power plants could be maintained. Unlike well-known estimation methods, this method does not need the development of a physical model, allows the processing of a large variety of materials (polymers, metallic alloys, and ceramics) and, above all, performs simultaneous estimation of both correlated thermophysical properties. Clearly, the results can be improved but they highlight the potential of such an approach. We manage to obtain mean relative errors between 8% (for the thermal diffusivity of polymers) and 20% (for the thermal conductivity of polymers and for both thermophysical properties of metallic alloys).
In this paper, we highlight that, when developing data-driven models, the training examples have to be carefully chosen. A reduced number of training examples or the addition to the training set of examples which do not provide useful information penalize generalization ability. Also, the length of the materials' thermophysical responses used as model inputs is critical. Its impact on performance has been evaluated and we highlight that 15-s long thermophysical responses are necessary to obtain good results.
It should be noted that the available database is rather small, which, of course, penalizes the development of estimation models based on machine learning. In addition, there is uncertainty over the properties' values given by manufacturers or taken from the literature. Because these values guide the weights and biases adjustment during training, the results summarized above are hopeful.
In order to continue this study, it would be crucial to consolidate the database, which will allow to increase the number of training examples and improve generalization ability. So, it would be possible to create a third class for materials with higher thermal conductivity, or even to distribute the available examples into more precise classes. Furthermore, it is necessary to precise the properties' values used as target values during training thanks to measurements. In addition, it is possible to conduct a similar study with an alternative input, as the temperature evolution on the materials' rear face, instead of such an evolution on the materials' front face. This input can bring additional information about the ability of the material to conduct heat through the thickness of the sample. Lastly, it is planned to test other machine learning tools as neuro-fuzzy systems. Considering the studies based on simulated data we conducted [20,21], it seems that these tools could improve the estimation results.
Acknowledgments
This work has received funding from the European Union's Horizon 2020 research and innovation program RAISELIFE under grant agreement No. 686008.
The authors would like to thank Goodfellow SARL for providing us samples, Hervé Duval (PROMES-CNRS) for his help in the instrumentation of the photothermal test bench, especially for the control of the laser, as well as Emmanuel Hernandez (PROMES-CNRS) for the shaping of the samples.
Author contribution statement
O. Faugeroux, B. Claudet and S. Grieu conceived of the presented idea. R. Reoyo-Prats carried out the experiment with support from O. Faugeroux and B. Claudet. R. Reoyo-Prats performed the numerical calculations and analyzed the data with support from S. Grieu. R. Reoyo-Prats and S. Grieu contributed to the final version of the manuscript. O. Faugeroux and B. Claudet supervised the project.
Appendix A
Thermal conductivity values according to various references.
Thermal diffusivity values according to various references.
References
- T. Kobari, J. Okajima, A. Komiya, S. Maruyama, Int. J. Heat Mass Transfer 91, 1157 (2015) [CrossRef] [Google Scholar]
- K.S. Reddy, S. Jayachandran, Int. J. Therm. Sci. 120, 136 (2017) [Google Scholar]
- I. Yang, D. Kim, S. Lee, Int. J. Heat Mass Transfer 122, 1343 (2018) [CrossRef] [Google Scholar]
- D.R. Thompson, S.R. Rao, B.A. Cola, J. Electron. Packag. 135, 1 (2013) [Google Scholar]
- M. Khandelwal, M.M. Mench, J. Power Sources 161, 1106 (2006) [Google Scholar]
- W.N. dos Santos, J. Eur. Ceram. Soc. 28, 15 (2007) [Google Scholar]
- S.E. Gustafsson, Rev. Sci. Instrum. 62, 797 (1991) [Google Scholar]
- B.M. Mihiretie, D. Cederkrantz, A. Rosén, H. Otterberg, M. Sundin, S.E. Gustafsson, M. Karlsteen, Int. J. Heat Mass Transfer 115, 216 (2017) [CrossRef] [Google Scholar]
- W.J. Parker, R.J. Jenkins, C.P. Butler, G.L. Abbott, J. Appl. Phys. 32, 1679 (1961) [Google Scholar]
- H.S. Carslaw, J.C. Jaeger, Conduction of Heat in Solids (Oxford University Press, 1959) [Google Scholar]
- R.D. Cowan, J. Appl. Phys. 34, 926 (1963) [Google Scholar]
- L.M. Clark, R.E. Taylor, J. Appl. Phys. 46, 714 (1975) [Google Scholar]
- K.B. Larson, K. Koyama, J. Appl. Phys. 38, 465 (1967) [Google Scholar]
- S. Min, J. Blumm, A. Lindemann, Thermochim. Acta. 455, 46 (2007) [Google Scholar]
- C.S.C. Pinto, H. Massard, P. Couto, H.R.B. Orlande, R.M. Cotta, M.C.R. Ambrosio, Brazilian Arch. Biol. Technol. 49, 31 (2006) [CrossRef] [Google Scholar]
- I.M. Abdulagatov, Z.Z. Abdulagatova, S.N. Kallaev, A.G. Bakmaev, Z.M. Omarov, J. Therm. Anal. Calorim. (2020). doi:10.1007/s10973-020-09765-x [Google Scholar]
- O. Faugeroux, Caractérisation thermophysique de revêtements de protection thermomécanique par méthode photothermique impulsionnelle, Ph.D. thesis, University of Perpignan Via Domitia, 2001 [Google Scholar]
- T.R. Pavlov, D. Staicu, L. Vlahovic, R.J.M. Konings, P. Van Uffelen, M.R. Wenman, Int. J. Therm. Sci. 124, 98 (2018) [Google Scholar]
- S. Orain, Y. Scudeller, S. Garcia, T. Brousse, Int. J. Heat Mass Transfer 44, 3973 (2001) [CrossRef] [Google Scholar]
- S. Grieu, O. Faugeroux, A. Traoré, B. Claudet, J.-L. Bodnar, Eur. Phys. J. Plus. 130, (2015). doi:10.1140/epjp/i2015-15241-y [Google Scholar]
- S. Grieu, O. Faugeroux, A. Traoré, B. Claudet, J.-L. Bodnar, Eur. Phys. J. Appl. Phys. (2015). doi:10.1051/epjap/2014140254 [Google Scholar]
- O. Faugeroux, S. Grieu, A. Traoré, J. Bodnar, B. Claudet, Outils de l'intelligence artificielle appliqués au CND, Tech. l'Ingénieur. 1, (2013) [Google Scholar]
- S. Brahim, J.L. Bodnar, P. Grossel, J. Phys. Conf. Ser. 214, (2010). doi:10.1088/1742-6596/214/1/012065 [Google Scholar]
- K. Hakem, M. Heuret, M. Egee, J. Phys. IV. 4, 51 (1994) [Google Scholar]
- S. Grieu, O. Faugeroux, A. Traoré, B. Claudet, J.L. Bodnar, Energy Build. 43, 543 (2011) [Google Scholar]
- GoodFellow, Catalogue et propriétés des matériaux, (n.d.). http://www.goodfellow.com (accessed September 9, 2019) [Google Scholar]
- Polyfluor, Matériaux − Fiches techniques, (n.d.). https://www.polyfluor.nl/fr (accessed September 9, 2019) [Google Scholar]
- IDM Composites, Matériaux − Fiches techniques, (n.d.). http://www.idmcomposites.com (accessed September 9, 2019) [Google Scholar]
- M. Laurent, P.-L. Vuillermoz, Conductivité thermique des solides, Tech. l'ingénieur. (1993) [Google Scholar]
- J.A. Brydson, in Plastics Materials, 7th edn (Butterwort, 1999) [Google Scholar]
- Professional Plastics Inc, Fiche technique, (n.d.). http://www.professionalplastics.com/ (accessed September 9, 2019) [Google Scholar]
- S. Laroze, J.-J. Barreau, Mécanique des structures, Edition Ma, 1988 [Google Scholar]
- Evonik Industries, Products − Technical information, (n.d.). https://www.plexiglas.de/product/plexiglas/en/products/plexiglas/pages/technical-information.aspx.html (accessedFebruary 3, 2017) [Google Scholar]
- MDS, Propriétés des matériaux, (n.d.). http://www.metaux-detail.com (accessed September 10, 2019) [Google Scholar]
- Castle MBA, Our product − MBA − UPVC, (n.d.). http://www.castle-mba.com/upvc/ (accessed September 17, 2019) [Google Scholar]
- Makeitfrom, Material properties database, (n.d.). https://www.makeitfrom.com/ (accessed September 10, 2019) [Google Scholar]
- HPC Europe, Fiches techniques, (n.d.). www.hpceurope.com (accessed September 10, 2019). [Google Scholar]
- J.-F. Bonnet, Polymères fluorés, Tech. l'Ingénieur. (2004) [Google Scholar]
- Plastiques Élastomères, Fiche technique, (n.d.). www.plastomere.com (accessed September 9, 2019) [Google Scholar]
- M. Chailly, Fiche technique, (n.d.). www.michaud-chailly.fr (accessed October 30, 2017) [Google Scholar]
- Ensinger, Fiche technique, (2018). www.ensingerplastics.com (accessed September 9, 2019) [Google Scholar]
- Euro métal Sud Ouest, Fiche technique, (n.d.). http://eurometalso.com/ (accessed September 9, 2019) [Google Scholar]
- Polytek, Propriétés du PEHD, (n.d.) [Google Scholar]
- P.S. Group, Fiche technique, (n.d.). http://www.plastiservice.com/FR/catalogue_produits (accessed September 9, 2019) [Google Scholar]
- Haynes International, Technical datasheet, (n.d.). www.haynesintl.com (accessed September 9, 2019) [Google Scholar]
- NeoNickel, Technical datasheet, (n.d.). https://www.neonickel.com/products/ (accessed September 9, 2019) [Google Scholar]
- Special Metals, Technical datasheet, (n.d.). http://www.specialmetals.com/assets/documents/alloys/inconel/inconel-alloy-625.pdf (accessed September 9, 2019) [Google Scholar]
- VDM Material international GmbH, VDM® Alloy 36 technical datasheet, (2018). https://www.vdm-metals.com/en/downloads/ (accessed September 9, 2019) [Google Scholar]
- FineTubes, Aciers inoxydables − Alliage 316, (2012). http://www.finetubes.fr/ [Google Scholar]
- L. Alloys, Alliage 316L, (n.d.). https://www.langleyalloys.com/fr/products/alloy-316l/ (accessed September 9, 2019) [Google Scholar]
- High Temp Metals, Kovar technical data, (n.d.). http://www.hightempmetals.com/techdata/hitempInvar36data.php (accessed September 9, 2019) [Google Scholar]
Cite this article as: Reine Reoyo-Prats, Stéphane Grieu, Olivier Faugeroux, Bernard Claudet, A novel ANN-based method for simultaneous estimation of thermophysical properties using experimental photothermal data, Eur. Phys. J. Appl. Phys. 93, 10901 (2021)
All Tables
Stability of the classification network depending on the photothermal response length and the number of hidden neurons, for the 4 example sets.
All Figures
 |
Fig. 1 The neural structure. |
| In the text | |
 |
Fig. 2 Network stability – determination of the inconsistent networks and outlier values. |
| In the text | |
 |
Fig. 3 Photothermal test bench at PROMES-CNRS. |
| In the text | |
 |
Fig. 4 Beginning of the PRBS sequence used excitation profile. |
| In the text | |
 |
Fig. 5 Examples of photothermal responses. |
| In the text | |
 |
Fig. 6 Impact on performance of the example sets. Left: Class 1. Right: Class 2. |
| In the text | |
 |
Fig. 7 Impact on performance of the photothermal response length. |
| In the text | |
 |
Fig. 8 Impact of the number of hidden neurons. |
| In the text | |
 |
Fig. 9 Estimation of properties and corresponding relative estimation errors for Class 1 and Class 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


