| Issue |
Eur. Phys. J. Appl. Phys.
Volume 89, Number 2, February 2020
|
|
|---|---|---|
| Article Number | 20901 | |
| Number of page(s) | 11 | |
| Section | Physics of Energy Transfer, Conversion and Storage | |
| DOI | https://doi.org/10.1051/epjap/2020190222 | |
| Published online | 17 April 2020 | |
https://doi.org/10.1051/epjap/2020190222
Regular Article
Estimation of the power flux supplied by an electric arc to Ag-SnO2 electrodes based on cross-section observations of the melted zone
1
Laboratoire GeePs, UMR CNRS-CentraleSupelec 8507, UPMC et Université Paris-Sud, 11 rue Joliot-Curie, 91192 Gif sur Yvette Cedex, France
2
MINES ParisTech, PSL University, Centre des Matériaux, CNRS UMR 7633, BP 87, 91003 Evry Cedex, France
3
Strategy & Innovation, Schneider Electric, 31 rue F. Quesnay, 38320 Eybens, France
* e-mail: romaric.landfried@centralesupelec.fr
Received:
26
July
2019
Received in final form:
5
December
2019
Accepted:
3
February
2020
Published online: 17 April 2020
A method is proposed to estimate the characteristics of the power flux supplied to an anode and a cathode in Ag-SnO2 submitted to an AC electric arc with a maximal value of the arc current intensity about 400–500 A and an arc duration about 4–5 ms. It is based on the one hand on the observation by optical microscopy and Electron BackScatter Diffraction (EBSD) of the area melted by the arc, thus making it possible to evaluate the depth and radius melted, and on the other hand on a thermal modelling allowing to estimate an equivalent voltage (proportionality coefficient between the intensity of the arc current and the received power) and the power flux surface density.
© A. Fouque et al., EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The design of contactors requires an understanding of many coupled physical phenomena (electrical, metallurgical, thermal, mechanical, etc.). Throughout the life of the component, the contact electrodes undergo numerous electrical arcs (ideally several hundred thousand) during the opening and closing operations of the contactor and are thus gradually damaged. These repeated actuations can lead to the failure of the component. For several years, Ag-SnO2 constitutes the best substitute to Ag-CdO as well for AC or DC switching. It has been shown [1] that using Ag-SnO2 may increase the contactor lifetime (in comparison with Ag-CdO). Degradation of contact electrodes results from various phenomena: welding of contact electrodes, prohibitive increase in contact resistance, evolution of the electrodes microstructure, partial or total destruction of the electrical contact materials (erosion, cracks, etc.) due to micro explosions, evaporation of electrode material, ejection of liquid droplets. This is illustrated in Figure 1 which shows a cross-section of an Ag-SnO2 contact pad after 50,000 openings with an arc current intensity of about 300 A rms. Bubbles and cracks can be observed in the material [2] as a result of melting-resolidification cycles of the pseudo-metal, as well as demixing areas between silver and tin oxide.
Numerous experimental studies [3–10] have been carried out so far on the degradation of Ag–SnO2 electrical contact materials in AC or DC cases. Most of them are focused on the erosion assessment, which may be done either by measuring the mass loss after a large number of arcs, or by observing the various craters and the evolution of the surface during the tests with an optical profilometer, for instance. To progress in the theoretical study and modelling of erosion phenomena, several steps are essential, notably a good knowledge of the properties of the contact material (thermal conductivity, electrical conductivity, hardness, etc.), and of the characteristics of the power flux brought to the electrode material. Different works concerning the first point have already been conducted [11,12]. The purpose of this paper is to address the second point by proposing a method for estimating the characteristics of the power flux supplied to Ag–SnO2 (88/12–wt.%) electrodes (i.e. the power and the surface power density). Several methods have already been proposed to estimate the power flux supplied by an arc to an electrode. Marotta et al. [13] have proposed a calorimetric method to estimate the power flux in the case of a plasma torch (copper electrodes). Hemmi et al. [14] proposed an indirect method from the mass loss measurement in the case of silver electrodes under the assumption that the entire mass loss is due to metal vaporization. Surface temperature measurement just after the arc extinction also allowed to estimate the power balance provided that the material emissivity is known [15]. Two other indirect methods have been proposed. The first one is based on the observation of craters (depth, radius, volume) left by an electric arc on the electrode surface [16] and the other one is based on the measurement, by centrifugation, of the molten metal created by the arc [17]. In this work we propose another method based on the observation after an opening arc of the electrode surface using a 3D optical profilometer and of the melted bath by optical and EBSD observations. Again, this is an indirect approach based on experimental results that uses simple modelling to obtain characteristics of the power flux brought to the electrodes.
The second section of the paper gives a description of the experimental device. The third section concerns the experimental observations made for Ag-SnO2 electrodes that have been exposed to a single electric arc. In a fourth section two methods are described for the exploitation of experimental results using a simple thermal model. In the fifth section, the results obtained using these two methods are presented, thus making it possible to highlight the qualities and defects of each of them. In a last section, a sensitivity study to the different parameters (material parameters or measurement parameters) is presented.
 |
Fig. 1 Cross section of an Ag-SnO2 contact electrode as observed using an optical microscope showing the degradation (bubbles, cracks, Ag and SnO2 demixing zone) after 50,000 arcs (I = 300 A rms). |
2 Description of the experimental device for electric tests
A schematic description of the electrical circuit considered in this work is shown in Figure 2. The power supply is an alternative voltage source (230 V rms at 50 Hz) which can deliver a current up to 600 A rms. The current value is fixed by the choice of the resistor value. The current in the circuit and the voltage measured between electrodes are recorded. The mobile part of the device is constituted of an electrode, a spring and a mobile electrode carrier. The spring ensures a contact force of 10 N. A laser measures the displacement of the mobile electrode carrier. At the beginning of this displacement, the applied force is progressively released while the contact remains closed. Then as soon as the applied force reaches 0, the contact opens at a constant speed (of around 0.4 m/s), and the displacement then corresponds to the electrode gap. The denomination ‘anode' or ‘cathode' for electrodes depends on whether the opening is made over a positive or negative half period. Indeed, in most cases, the arc is extinguished when the current flows to zero. There is no re-striking and therefore the electrodes do not change their polarity during the arc.
An example of current, voltage and displacement recorded is shown in Figure 3. The phase difference between current and tension resulting from (R,L) circuit cannot be seen on this graph. A calculator (Labview real time) takes into account the spring characteristics so that the displacement of the mobile electrode carrier causes an opening leading to a 4 ms arc duration. The mobile part begins moving at about 6 ms. At 14 ms, the contact is effectively opening and an arc is generated. The arc extends until it is extinguished when the current reaches zero at around 18 ms.
In Figure 4 is presented a schematic view of the electrode (static and mobile) structure showing the different layers with their respective thickness. The contact material Ag-SnO2 is separated from Cu substrate by Ag and braze layers. It is produced by PSR (Press Sinter Repress) from a powder obtained by co-precipitation, as described in [18].
In the work presented below we will focus on a 300 A rms current intensity.
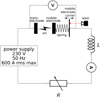 |
Fig. 2 Electrical circuit diagram; three values of resistances are used to get three current values of 150, 300 and 600 A rms; the inductance value is set to get cos(ϕ) = 0.35. |
 |
Fig. 3 Typical oscillogram of (a) current intensity, (b) contact voltage and (c) displacement of the mobile electrode carrier with a 150 A rms current; (1) mobile electrode carrier displacement begins, (2) contact opening and arc appearance, (3) arc quenching. |
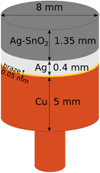 |
Fig. 4 Schematic representation of the different layers constituting the electrodes (static and mobile). |
3 Damages caused by a single arc
As recalled in the introduction section a classic way to study electrode erosion by arcing is to measure mass loss. This approach has the advantage of statistical methods since it consists in averaging over several tens, hundreds or even thousands of arcs the mass loss of the electrodes related to droplet ejections or material vaporization. However, it does not allow to see in detail, at the surface level, the damage created by each arc. Another method, used here, is based on surface observation by optical profilometry [19]. This is particularly useful in the case of a single arc, but has the disadvantage of not providing an average representation of the behavior of an arc. The observation of traces (craters) left by an arc on the surface of an electrode is of great interest: this gives access to the depths and radii of the craters formed under the action of the electric arc. It is also possible to quantify the volumes of material moved, which is an important contribution compared to the traditional electrode weighting method, which does not show the amount of material moved, but only the amount lost.
Similarly, we can easily observe the roughness and deformations of the surface caused by the arc action and thus make hypotheses about the small-scale mobility of the arc foot, which is not always easy to observe with a fast camera.
The arcs are carried out on a contact consisting of a dome-shaped electrode and a flat electrode. The latter will be observed with a profilometer. In the following we present two examples concerning two distinct arcs for two different plane electrode polarities. As we will see later, the arc current intensities will not be exactly the same.
3.1 Case of an Ag-SnO2 anode
In Figure 5 the evolution of the arc current intensity (red) and of the arc voltage (black) are presented. This current evolution will be used for the modelling phase presented in Section 4 (Eq. (1)). Figure 6 presents a top view (obtained by 3D profilometry) of the crater created by such an arc as well as a surface profile measured along a crater diameter. It can be deduced from these images that the molten diameter is at least equal to the distance between points R and M, i.e. about 1 mm, and that the molten depth is at least equal to 25 μm.
Moreover, to get insight into different phenomena occurring during a single arc, the bulk of the samples close to the surface was observed using an optical microscope. The samples were cut along a diameter of the crater and further prepared by standard metallographic techniques. To limit the sample damage during the sample preparation and, thus, that of resulting crater geometry, a low-speed wire saw cutting was used. The crater diameter measured using obtained cross-section and observed by optical microscopy was systematically compared with that measured using 3D optical profilometry. An excellent agreement between both values indicated that the cutting was carried out successfully in the center of the crater. After polishing, a chemical etching (mix of ammoniac and hydrogen peroxide) was applied to reveal the cathode microstructure features. A change in the appearance of the material was observed on a lenticular sub surface volume whose dimensions are 1525 μm in diameter and 175 μm in depth (Fig. 7).
To understand the origin of the contrast change in the subsurface area in Figure 7, an analysis by electron backscatter diffraction (EBSD) was carried out. Inverse pole figure map for silver obtained in the normal direction to the sample cross-section is presented in Figure 8. Each color in such a map corresponds to a specific crystalline orientation of the silver lattice, according to the triangle of orientation. Therefore, each individual grain appears as single color object. We can observe that the initial microstructure (not affected by the arc) consists of relatively small grains (not well resolved in Fig. 7). By contrast, the sub surface area under the crater center reveals large Ag grains of different morphology with the largest grains of hundred microns in the largest dimension. Such a grain structure is typical for solidification of metals with the elongation direction of grains parallel to the temperature gradient [20]. It suggests that the area containing large grains revealed by EBSD was melted by the arc. It is worth noting, that due to a very short arc action, we do not expect any significant Ag grain growth controlled by diffusion and all revealed microstructure changes as compared to initial state are attributed thus to melting with subsequent resolidification. The dimensions of the melted area thus observed are 1415 μm for the diameter and 185 μm for the depth.
 |
Fig. 5 Evolution of arc current intensity (red) and arc voltage (black). |
 |
Fig. 6 Left: top view of an Ag-SnO2 anode surface after the single arc of Fig. 5 obtained by 3D optical profilometry. Right: 2D surface profile obtained along blue line in the figure on the left showing the displaced molten material. |
 |
Fig. 7 Anode microstructure in the cross section along a crater diameter after a single arc (300 A rms current − case of a flat anode), observed with an optical microscope. |
 |
Fig. 8 Inverse pole figure map for silver obtained in the normal direction to the sample cross-section of an anode cross section along a crater diameter after a single arc (300 A rms current). |
3.2 Case of an Ag-SnO2 cathode
A similar approach was used for a cathode for which the arc current, the topographic survey obtained by 3D profilometry, as well as microstructure observations carried out by optical microscopy and EBSD are presented in Figures 9–12.
In these conditions, the minimum diameter of molten material under the reference surface (in dashed line in Fig. 12) is around 1100 μm. The dimensions of the melted volume obtained from optical observation (Fig. 11) are 1900 μm in diameter and 200 μm in depth and the dimensions of the melted area thus observed by EBSD (Fig. 12) are 1850 μm for the diameter and 220 μm for the depth.
Such observations make it possible to obtain the position of the melted front and to quantify the volume of molten material under the arc action. Moreover, comparison of observations obtained in 3D profilometry and EBSD or optical microscopy show that only a small amount of the molten liquid was set in motion and ejected from the crater under the action of the various arc-related forces (Laplace and Marangoni). In [21] the authors studied the Marangoni effect and showed that in the case of Ag electrodes, the movement of the molten bath by the Marangoni effect was rapid: in their case they estimated a surface velocity related to this effect of about 3.6 m/s after 1 ms over a thickness of 17 μm and 7 m/s after 10 ms over a thickness of 24 μm. They also showed that the value of the velocity reached at the surface varied in 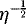 where η is the viscosity. Then this is certainly due to the high viscosity of Ag-SnO2 compared to Ag as it has been observed with a laser cinematography system allowing to see the motion of the liquid metal at the electrode surface [22].
where η is the viscosity. Then this is certainly due to the high viscosity of Ag-SnO2 compared to Ag as it has been observed with a laser cinematography system allowing to see the motion of the liquid metal at the electrode surface [22].
 |
Fig. 9 Evolution of arc current intensity (red) and arc voltage (black). |
 |
Fig. 10 Left: top view of an Ag-SnO2 cathode surface after the single arc of Figure 9 obtained by 3D optical profilometry. Right: 2D surface profile obtained along blue line in the figure on the left showing the displaced molten material. |
 |
Fig. 11 Cathode microstructure in the cross section along a crater diameter after a single arc (300 A rms current − case of a flat cathode), observed with an optical microscope. |
 |
Fig. 12 Inverse pole figure map for silver obtained in the normal direction to the sample cross-section of a cathode cross section along a crater diameter after a single arc (300 A rms current). |
4 Methods to determine the characteristics of the power flux using microstructure observations and a thermal model
In this part two methods will be proposed to determine the characteristics of the power flux from the results presented in Section 3. The first one, based on 3D profilometry measurements, has already been described previously in reference [16], therefore only its broad outlines will be presented here. The second one, involving observations made on the electrode cross sections, is proposed for the first time, thus more details will be given. But first of all, it is necessary to explain the approach we have chosen regarding the description of the power balance at the electrodes and of the model used to describe the arc-electrode interaction and then the electrode heating.
4.1 Recalling concerning the power balance at the electrode
In our approach, the interactions between the different particles (ions, neutral species and electrons) and the electrode surface at a microscopic scale are not explicitly taken into account. A macroscopic point of view for the arc root structure is adopted. Several authors [23–25] have already used a similar description. In these conditions the macroscopic power balance is expressed by way of a ‘voltage equivalent’ parameter called Veq
. Two simple relations are used to express the power and the surface power density received by an electrode: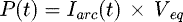 (1)
(1)
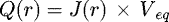 (2)
(2)
where P is the power brought to the electrode surface (PA for an anode and PC for a cathode), Q is the surface power density brought to the electrode (QA for an anode and QC for a cathode), Iarc (t) the arc current intensity, Veq is a voltage equivalent parameter at the electrode (VeqA for an anode and VeqC for a cathode), J is the arc current density at the electrode arc root (JA for an anode and JC for a cathode). Under these conditions it is assumed that the power supplied to the electrodes varies proportionally with the arc current. As in many cases, Veq is assumed to be constant. However, it should be noted that Benilov et al. [26,27] proposed an evolution of Veq during the arc. The main physical limitation of this macroscopic approach (use of Veq ) may be the arc duration and the environment pressure. Indeed, in the case of very short arc duration or in the case of a vacuum arc with several separated microspots on the cathode surface for instance, a microscopic approach should be considered.
The model, already described in reference [16], has the following characteristics: the arc root on the electrodes is considered as immobile, the problem will therefore have an axisymmetric geometry; the heating related to the Joule effect is neglected; the values of the equivalent voltages as well as those of the power flux-density surfaces will be independent of time. Thus we will have the following simple expressions linking the radius of the arc root a(t), the current density and the arc current intensity :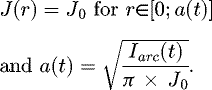 (3)
(3)
As regards the boundary conditions, the cylindrical electrode is heated at the top by the power flux. On the lateral edges, cooling by convection and radiation will be neglected (this is justified by the short duration of the arc considered ≈ 4 ms). The height of the electrode is high enough to consider that the bottom of the electrode remains at a constant temperature during the arc. Solving the heat equation then makes it possible to obtain the evolution of the temperature distribution in the electrode during the arc. Phase changes (melting and vaporization) are taken into account. The values of the characteristics of the Ag-SnO2 material are extracted from reference [12] for the properties of the solid material where they were obtained experimentally. For the properties of the liquid material, we have taken those proposed in reference [11] obtained by modelling and which will be discussed later.
4.2 Method using 3D profilometry observations (called method 1)
The observations by 3D profilometry made it possible to obtain minimum values of the molten radius (rmin
) and molten depth (dmin
) during the arc. Thus, our approach consisted in searching for the values of (Veq, Q) which, through simulation, lead to calculated fused radii (rcal
) and calculated fused depths (dcal
) respectively higher than rmin
and dmin
. This therefore gives two constraints in order to determine the couples (Veq, Q) making simulations and experimental observations compatible. This is expressed simply by writing the two criteria denoted C
1 and 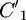 that must be satisfied:
that must be satisfied: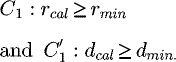
4.3 Method based on microstructure observations (called method 2)
The simulation results have also been compared with melted depths (dmel
) and melted radii (rmel
) measured optically or from EBSD maps. It is worth noting that optical and EBSD observations lead to slightly different values for melted radii and melted depths. We have set ourselves two criteria to select the value pairs (Veq, Q) that we considered to be compatible. One (denoted C
2) refers to the melted radius, the other (denoted 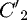 ) to the depth. Thus we have sought to simultaneously minimize two quantities, namely:
) to the depth. Thus we have sought to simultaneously minimize two quantities, namely:
The “average measured melted radius or depth” is the average between the values obtained by optical microscopy and EBSD. In view of the differences in values given by both methods used, we have set ourselves the following criteria C
2 and 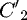 which are Δr/r and Δd/d ≤ 15%.
which are Δr/r and Δd/d ≤ 15%.
5 Results obtained with both methods for Ag-SnO2 electrodes
5.1 Results obtained for an Ag-SnO2 anode
5.1.1 Method 1
In Figure 13 we have drawn in green, in the (Veq, Q) plan, the area describing all the couples leading to simulated values for fused radii and fused depths compatible with the criteria C
1 and 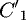 for the anode case.
for the anode case.
 |
Fig. 13 Compatibility zone between model and experience in the axes (Veq , Q) with criteria compatibility C 1 and C 1’– Case of an Ag-SnO2 anode. |
5.1.2 Method 2
In Figure 14 we have drawn in red, in the (Veq
, Q) plan, the area describing all the couples leading to simulated values for fused radii and fused depths compatible with the criteria C
2 and 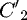 . Schematically, VeqA
is in the range 4.1–7.6 V and QA
in the range 5.6 108 to 8.4 108 W/m2.
. Schematically, VeqA
is in the range 4.1–7.6 V and QA
in the range 5.6 108 to 8.4 108 W/m2.
The Figure 15 allows to compare the extension of the two compatibility zones according to the choice of the criteria.
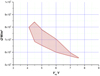 |
Fig. 14 Compatibility zone between model and experience in the axes (Veq , Q) with criteria compatibility C 2 and C 2’ − Case of an Ag-SnO2 anode. |
 |
Fig. 15 Compatibility zones obtained with the two types of criteria − Case of an Ag-SnO2 anode. |
5.2 Results obtained for an Ag-SnO2 cathode
In Figure 16 we have drawn in green and red, in the (Veq
, Q) plan, the areas describing all the couples leading to simulated values for fused radii and fused depths compatible with the criteria C
1 and 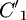 (in green) and C
2 and
(in green) and C
2 and 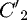 (in red). A zoom of the zone obtained according criteria C
2 and
(in red). A zoom of the zone obtained according criteria C
2 and 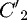 is proposed in Figure 17. Schematically, VeqC
is in the range 7–12 V and QC
in the range 6.5 108–8.5 108 W/m2.
is proposed in Figure 17. Schematically, VeqC
is in the range 7–12 V and QC
in the range 6.5 108–8.5 108 W/m2.
 |
Fig. 16 Compatibility zones obtained with the two types of criteria − Case of an Ag-SnO2 cathode. |
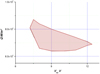 |
Fig. 17 Zoom of the compatibility zone between model and experience in the axes (Veq
, Q) according to criteria C
2 and |
6 Discussion
The compatibility zone obtained using method 1 is much larger than that obtained by method 2, which is obviously included in the former. In addition, the constraints proposed by method 1 do not make it possible to limit the area along the Veq axis. In the rest of the article we will discuss the results obtained by method 2. In this section the discussion will focus on the influence that various parameters can have on the final results. This will thus make it possible to draw attention to the precautions to be taken in the application of both methods and also to suggest possible improvements. The various points that will be discussed are as follows :
-
The relevance of the hypothesis concerning relative immobility of the arc root. Unlike what happens in a conventional contactor, the geometry of the experimental device has been chosen in such a way as to minimize the displacement of the arc root during the experiment. However, very often, the arc can move due to its own instability (all the more important as the intensity of the current will be greater). Moreover, since the inter-electrode distance is small (in the order of mm), it is particularly difficult to observe the precise displacement of the arc. Only the observation of the trace left by the arc on the electrode surface can indicate the existence of a movement without giving us any information on speed. Thus, if we return to the two examples previously taken, in the case of Figure 6 we have observed a crater with a pronounced axisymmetric aspect, while in the case of Figure 10, we see that the crater has a slightly elongated shape. In the second case, assuming a stationary arc will certainly lead to an “error” in the final result.
-
The accuracy of the material cut position before optical and EBSD observations. Again, we cannot expect to cut the pad exactly along a crater diameter. The measurement of the fused radius will then be affected by a certain error. The same will apply to the value of the melted depth, which can also be minimized.
-
The thermodynamic properties of the material in its liquid phase, such as thermal conductivity, thermal diffusivity, etc.
6.1 Estimation of the influence of the relative immobility of the arc root and the influence of the position of the cross section
The short duration of the arcs (a few ms), as well as the absence of a system for setting the arc root in motion (shape of the current feeds for example), are important arguments justifying the use of a 2D axisymmetric model. However, observation of the crater shows that this axisymmetric character is not always perfectly followed. Precise observation of the arc displacement is made particularly difficult by high brightness of the arc and low inter-electrode distance. However, the arc root can move a few tens of microns during the arc. Due to arc root movement, the measured depth of the melted volume will be underestimated while the measured radius of this volume will be overestimated. Regardless of the question of the immobility of the arc, the question arises of the precision with which the cut made for optical and EBSD observations could be made. Depending on the positioning of the cut, the values of the melted radius and melted depth will vary. Generally speaking, in the ideal case of a stationary arc, a shift in the cut will lead to an underestimation of the melted depth and radius.
To simulate the influence of these two parameters, we studied the changes caused by slight variations in the melted depth and melted radius on the compatibility zone. Four configurations were chosen: a melted radius equal to ±10% of the measured value and a melted depth equal to ±10% of the measured value.
In Figures 18 and 19 modified compatibility zones have been plotted in order to estimate the influence of variations in the values of the melted radius and melted depth, respectively, in the case of an anode. The zone obtained with initial values, previously plotted in Figure 14, has been recalled.
Similar figures have been plotted in the case of a cathode in Figures 20 and 21.
It appears that a change in the value of the melted radius mainly affects the Veq value, while a change in the value of the melted depth especially affects the value of Q.
 |
Fig. 18 Compatibility zones (case of an anode) obtained in three cases: with initial values of the melted depth and radius (in red), with initial values of the melted depth and an increase of 10% of the melted radius (in blue), with initial values of the melted depth and a decrease of 10% of the melted radius (in green). |
 |
Fig. 19 Compatibility zones (case of an anode) obtained in three cases: with initial values of the melted radius and depth (in red), with initial values of the melted radius and an increase of 10% of the melted depth (in orange), with initial values of the melted radius and a decrease of 10% of the melted depth (in purple). |
 |
Fig. 20 Compatibility zones (case of a cathode) obtained in three cases: with initial values of the melted depth and radius (in red), with initial values of the melted depth and an increase of 10% of the melted radius (in blue), with initial values of the melted depth and a decrease of 10% of the melted radius (in green). |
 |
Fig. 21 Compatibility zones (case of a cathode) obtained in three cases: with initial values of the melted radius and depth (in red), with initial values of the melted radius and an increase of 10% of the melted depth (in orange), with initial values of the melted radius and a decrease of 10% of the melted depth (in purple). |
6.2 Influence of the properties considered for the melted material (example of anode case)
Thermodynamic properties of the material in the solid state have been obtained in reference [12]. These measurements were made for the solid phase of the material, i.e. up to the melting temperature of Ag. Beyond this temperature it is particularly difficult to measure thermodynamic properties when the material changes to liquid phase. Some authors [11,28] have proposed simple models to estimate the properties of Ag-SnO2 beyond the melting point of Ag. In our work higher temperature properties are extracted from reference [11] and have not been validated experimentally.
However, it is essential to study the influence of these values on the two parameters of interest: the radius and the depth of the fused zone. For this purpose, we have chosen a couple of values in the compatibility range given in Figure 14 (5.5 V; 6.75 108 W/m2) and have plotted in Figures 22 and 23 the values of parameters Δr/r and Δd/d versus the relative variation of the specific heat in the molten material and the relative variation of the thermal conductivity of the molten material. The relative variations are defined as follows: 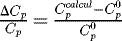 and
and 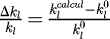 , where
, where 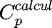 (respectively
(respectively 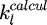 ) is the value of the specific heat value (respectively the thermal conductivity) used for the calculation and
) is the value of the specific heat value (respectively the thermal conductivity) used for the calculation and 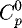 (respectively
(respectively 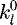 ) the specific heat value (respectively the thermal conductivity) proposed in reference [11].
) the specific heat value (respectively the thermal conductivity) proposed in reference [11].
The two parameters (Δr/r and Δd/d) are not very sensitive to specific heat variations: in the two cases they remain inferior to 15% (dashed line in Fig. 23). The dependence on the thermal conductivity variations is more important (in particular regarding the melted depth) and this highlights the need to characterize the material in its liquid phase in order to get more accurate estimations of the power flux.
 |
Fig. 22 Δr/r and Δd/d versus the relative variation of the specific heat in the molten material. |
 |
Fig. 23 Δr/r and Δd/d versus the relative variation of the thermal conductivity in the molten material. |
7 Conclusion
A new method has been proposed to estimate the characteristics of the power flux supplied to Ag-SnO2 contact electrodes. Profilometric analysis of the electrodes surfaces and microstructure observations using optical microscopy and EBSD made it possible to estimate the crater shape and the dimensions of the molten zone. The dimensions thus obtained serve as convergence criteria in solving the inverse problem of estimating a power flux making the model and experiment compatible. The use of the dimension of the molten zones is more fruitful than the use of the crater shape. Then, in the case of an anode Veq was found in the range 4.1–7.6 V and Q in the range 5.6 108–8.4 108 W/m2. In the case of a cathode Veq was found in the range 7-12 V and Q in the range 6.5 108–8.5 108 W/m2.
However, attention must be paid to different points. The immobility (or mobility) of the arc root during opening phase and the accuracy of the cut of the material made in order to observe the molten area are two factors that may cause noticeable changes in Veq and Qmax values. In addition, it seems important to accurately characterize the properties of the material at high temperature and more particularly its thermal conductivity.
Acknowledgments
This work has benefited from the financial support of the LabeX LaSIPS (ANR-10-LABX-0040-LaSIPS) managed by the French National Research Agency under the “Investissements d'avenir” program (n°ANR-11-IDEX-0003-02).
References
- J.L. Wintz et al., in Proceedings of the 59th Holm Conference on Electrical Contacts (2013), pp. 135–144 [Google Scholar]
- S. Kang et al., IEEE Trans. Comp. Hybrids Manuf. Technol. 12 , 32 (1989) [CrossRef] [Google Scholar]
- M. Zhang et al., Trans. Nonferrous Met. Soc. China 26 , 783 (2016) [CrossRef] [Google Scholar]
- J. Swingler et al., IEEE Trans. Comp. Hybrids Manuf. Technol. A 19 , 404 (1996) [Google Scholar]
- M. Hasegawa et al., in Proceedings of the 59th IEEE Holm Conference on Electrical Contacts (2013), pp. 288–294 [Google Scholar]
- C. Leung et al., in Proceedings of the 50th IEEE Holm Conference on Electrical Contacts (2004), pp. 64–69 [Google Scholar]
- H. Jiang et al., in 3rd Int. Conf. on Electric Power Equipment − Switching Technology (ICEPE-ST) (2015) [Google Scholar]
- J. Shea, in Proceedings of the 54th IEEE Holm Conference on Electrical Contacts, 2008 [Google Scholar]
- M. Hasegawa et al., in Proceedings of IEEE Holm Conference on Electrical Contacts (2012), pp. 280–286 [Google Scholar]
- A.M. Gouega et al., Eur. Phys. J. Appl. Phys. 11 , 111 (2000) [CrossRef] [EDP Sciences] [Google Scholar]
- A. Bonhomme, Ph.D thesis, Ecole Nationale Supérieure des Mines de Nancy, 2005 [Google Scholar]
- A. Fuentes, Ph.D thesis, Bretagne Sud University, 2010 [Google Scholar]
- L.I. Sharakhovsky et al., J. Phys. D: Appl. Phys. 30 , 2018 (1997) [CrossRef] [Google Scholar]
- R. Hemmi et al., J. Phys. D: Appl. Phys. 36 , 1097 (2003) [CrossRef] [Google Scholar]
- R. Landfried et al., IEEE Trans. Plasma Sci. 40 , (2012) [Google Scholar]
- Ph. Teste et al., Plasma Sources Sci. Technol. 17 , 035001 (2008) [Google Scholar]
- R. Landfried et al., Eur. Phys. J. Appl. Phys. 66 , 20801 (2014) [CrossRef] [EDP Sciences] [Google Scholar]
- P. Braumann, A. Koffler, in Proceedings of IEEE Holm Conference on Electrical Contacts (2004) pp. 90–97 [Google Scholar]
- D. Zhang et al., IEEE Trans. Comput. Pack. Technol. 29 (2006) [Google Scholar]
- D.A. Porter, K.E. Easterling, Phase transformation in metals and alloys, 6th ed. (2006) [Google Scholar]
- J.-P. Chabrerie, L. Boyer, Proceedings of the 13th International Conference on Electrical Contacts (1986), pp. 96–100 [Google Scholar]
- J. Devautour, Ph.D thesis, Paris 6 University, 1992 [Google Scholar]
- H. Salihou et al., J. Phys. D: Appl. Phys. 28 , 1883 (1995) [CrossRef] [Google Scholar]
- N.A. Sanders et al., J. Appl. Phys. 55 , 714 (1984) [Google Scholar]
- J. Devautour et al., J. Phys. 3 , l157 (1993) [Google Scholar]
- M.S. Benilov, A. Marotta, J. Phys. D : Appl. Phys. 28 , 1869 (1995) [CrossRef] [Google Scholar]
- M.S. Benilov, M.D. Cunha, J. Phys. D : Appl. Phys. 36 , 603 (2003) [CrossRef] [Google Scholar]
- M. Sun et al., IEEE Trans. Comp. Pack. Manufactur. Technol. A 17 , 490 (1994) [CrossRef] [Google Scholar]
Cite this article as: Aurélien Fouque, Alexandre Bonhomme, Georges Cailletaud, François Chaudot, Vladimir A. Esin, Frédéric Houzé, Romaric Landfried, Marina Lisnyak, Jean-Luc Ponthenier, Philippe Testé, Estimation of the power flux supplied by an electric arc to Ag-SnO2 electrodes based on cross-section observations of the melted zone, Eur. Phys. J. Appl. Phys. 89, 20901 (2020)
All Figures
 |
Fig. 1 Cross section of an Ag-SnO2 contact electrode as observed using an optical microscope showing the degradation (bubbles, cracks, Ag and SnO2 demixing zone) after 50,000 arcs (I = 300 A rms). |
| In the text | |
 |
Fig. 2 Electrical circuit diagram; three values of resistances are used to get three current values of 150, 300 and 600 A rms; the inductance value is set to get cos(ϕ) = 0.35. |
| In the text | |
 |
Fig. 3 Typical oscillogram of (a) current intensity, (b) contact voltage and (c) displacement of the mobile electrode carrier with a 150 A rms current; (1) mobile electrode carrier displacement begins, (2) contact opening and arc appearance, (3) arc quenching. |
| In the text | |
 |
Fig. 4 Schematic representation of the different layers constituting the electrodes (static and mobile). |
| In the text | |
 |
Fig. 5 Evolution of arc current intensity (red) and arc voltage (black). |
| In the text | |
 |
Fig. 6 Left: top view of an Ag-SnO2 anode surface after the single arc of Fig. 5 obtained by 3D optical profilometry. Right: 2D surface profile obtained along blue line in the figure on the left showing the displaced molten material. |
| In the text | |
 |
Fig. 7 Anode microstructure in the cross section along a crater diameter after a single arc (300 A rms current − case of a flat anode), observed with an optical microscope. |
| In the text | |
 |
Fig. 8 Inverse pole figure map for silver obtained in the normal direction to the sample cross-section of an anode cross section along a crater diameter after a single arc (300 A rms current). |
| In the text | |
 |
Fig. 9 Evolution of arc current intensity (red) and arc voltage (black). |
| In the text | |
 |
Fig. 10 Left: top view of an Ag-SnO2 cathode surface after the single arc of Figure 9 obtained by 3D optical profilometry. Right: 2D surface profile obtained along blue line in the figure on the left showing the displaced molten material. |
| In the text | |
 |
Fig. 11 Cathode microstructure in the cross section along a crater diameter after a single arc (300 A rms current − case of a flat cathode), observed with an optical microscope. |
| In the text | |
 |
Fig. 12 Inverse pole figure map for silver obtained in the normal direction to the sample cross-section of a cathode cross section along a crater diameter after a single arc (300 A rms current). |
| In the text | |
 |
Fig. 13 Compatibility zone between model and experience in the axes (Veq , Q) with criteria compatibility C 1 and C 1’– Case of an Ag-SnO2 anode. |
| In the text | |
 |
Fig. 14 Compatibility zone between model and experience in the axes (Veq , Q) with criteria compatibility C 2 and C 2’ − Case of an Ag-SnO2 anode. |
| In the text | |
 |
Fig. 15 Compatibility zones obtained with the two types of criteria − Case of an Ag-SnO2 anode. |
| In the text | |
 |
Fig. 16 Compatibility zones obtained with the two types of criteria − Case of an Ag-SnO2 cathode. |
| In the text | |
 |
Fig. 17 Zoom of the compatibility zone between model and experience in the axes (Veq
, Q) according to criteria C
2 and |
| In the text | |
 |
Fig. 18 Compatibility zones (case of an anode) obtained in three cases: with initial values of the melted depth and radius (in red), with initial values of the melted depth and an increase of 10% of the melted radius (in blue), with initial values of the melted depth and a decrease of 10% of the melted radius (in green). |
| In the text | |
 |
Fig. 19 Compatibility zones (case of an anode) obtained in three cases: with initial values of the melted radius and depth (in red), with initial values of the melted radius and an increase of 10% of the melted depth (in orange), with initial values of the melted radius and a decrease of 10% of the melted depth (in purple). |
| In the text | |
 |
Fig. 20 Compatibility zones (case of a cathode) obtained in three cases: with initial values of the melted depth and radius (in red), with initial values of the melted depth and an increase of 10% of the melted radius (in blue), with initial values of the melted depth and a decrease of 10% of the melted radius (in green). |
| In the text | |
 |
Fig. 21 Compatibility zones (case of a cathode) obtained in three cases: with initial values of the melted radius and depth (in red), with initial values of the melted radius and an increase of 10% of the melted depth (in orange), with initial values of the melted radius and a decrease of 10% of the melted depth (in purple). |
| In the text | |
 |
Fig. 22 Δr/r and Δd/d versus the relative variation of the specific heat in the molten material. |
| In the text | |
 |
Fig. 23 Δr/r and Δd/d versus the relative variation of the thermal conductivity in the molten material. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.