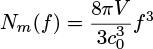| Issue |
Eur. Phys. J. Appl. Phys.
Volume 99, 2024
|
|
|---|---|---|
| Article Number | 2 | |
| Number of page(s) | 7 | |
| DOI | https://doi.org/10.1051/epjap/2023230152 | |
| Published online | 02 February 2024 | |
https://doi.org/10.1051/epjap/2023230152
Original Article
Fuel ignition using remote generation of microwave plasma in air at atmospheric pressure★
1
ONERA/DMPE, Université de Toulouse,
F-31055
Toulouse, France
2
LAPLACE, CNRS, Université de Toulouse,
Toulouse, France
* e-mail: Beatrice.Fragge@hotmail.com
Received:
8
August
2023
Accepted:
22
November
2023
Published online: 2 February 2024
The high demand for a new ignition device for aeronautical engines has motivated the study on an innovative microwave approach, presented in this paper. A dedicated experimental set-up is presented in which we demonstrate the successful ignition of a kerosene spray by a remotely excited microwave plasma. This plasma is created in a Split Ring Resonator (SRR) gap, placed in a copper cavity, in air at atmospheric conditions at the frequency of f = 2.8467 GHz and a pulsed power injected into the cavity of Pcav ≈ 1500 W.
Key words: Fuel ignition / Microwave plasma / Time reversal / Split Ring Resonator / Combustion chamber
Supplementary material is available in electronic form at https://www.epjap.org/10.1051/epjap/2023230152/olm
© B. Fragge et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Since the beginning of thermal engines in the automobile and aeronautical industries, spark plugs are used to ignite the fuel/air mixture. Such a system is robust and cheap, but there are a couple of disadvantages for aeronautical gas turbines such as the relight problem in critical conditions. These conditions refer to the relight of a plane engine at high altitude (0.2 bar, −56 °C) or the cold start of a helicopter engine under mountain conditions (e.g. 0.47 bar, −24 °C). Besides, the new environmental and economic restrictions lead to consider new engine regimes, such as very low mixture ratios for which the spark plug is not the most adapted system. Over 50 years of research for an alternative system has provided a huge number of approaches. Most of them use a nonequilibrium plasma [1–3]. These plasmas have a positive influence, e.g. in terms of flame stabilization and flame speed enhancement [4,5]. The most popular approaches are based on laser ignition [6,7], radio frequency discharge [4,8], impulse nanosecond discharge [9,10] and microwave ignition [11,12]. The approach presented in this paper is part of the latter. This principle is very promising since it could promote a spatial AND temporal control of the energy focal point by shaping the temporal variations of the microwave signal [13]. Recent developments in the use of time reversal to control the ignition of plasmas [14] make us think about the way it could be used to engine fuel ignition.
As a first step towards this goal, we use Split Ring Resonators (SRRs) to focus the deposited energy with a continuous wave signal. These concentrators in this paper are replacing the time reversal conventional method.
In the microwave literature, SRRs are often found in the context of metamaterials, where they are used to produce the desired magnetic susceptibility of the material [15]. In recent studies, they have been coupled to plasmas to achieve special characteristics such as negative permittivity and permeability [16–18]. One of the first to create a microplasma in the gap of the SRR were Iza et al. [19]. They did experiments in Argon and air at low pressures (1–20 Torr for air and 1–70 Torr for argon). Later Dextre et al. [20] studied the influence of geometric parameters on microwave plasma properties. In these studies [19,20], the SRRs are excited via a coaxial cable welded directly on the SRRs. Singh et al. [21] showed first its remote excitation in free space and the creation of plasmas under these conditions.
However, several steps are necessary to bring this system inside an aeronautical combustion chamber. At first, we need to verify that a plasma can be created in air at ambient conditions and to demonstrate the ignition of kerosene (aeronautical fuel Jet A1) thanks to this plasma.
In summary, the article presents “new” experiments where plasma is created in the SRR’s gap in air at Patm with a pulsed sinusoidal microwave signal to ignite kerosene. After a description of the experimental set-up and its characteristics, more details are given about the plasma creation on the SRRs and the ignition of a kerosene spray. These results will pave the way for future tests where application of the time reversal principle will enable to create and control the plasma in both, space and time.
2 Experimental set-up
2.1 The electromagnetic cavity
For this study, a dedicated electromagnetic, reverberant cavity has been designed, see Figure 1. This cavity represents in a very simplified way a combustion chamber in which we want to ignite a spray of kerosene via time reversal. It has to integrate not only the components to inject the fuel and the microwaves, but also measurement devices. In the following, are listed the principal choices that led to the final design:
the creation of a microwave plasma at ambient pressure in air needs a high electric field and therefore a high microwave power. The microwave material at our disposition allowed to create such a high power in a bandwidth up to 3 GHz. The minimum wavelength (at 3 GHz) is 10 cm.
To maximise the efficiency of the time reversal, i.e. maximisation of the energy stored in the cavity, one needs highly reflecting walls. This is the reason for choosing copper plates that have a very good conductivity.
-
The time reversal needs a high number of electromagnetic modes inside the cavity to reach a high quality in terms of spatial and temporal focusing [22]. Following the equation of Weyl, this number of modes increases with the volume depending on the frequency as:
with Nm the number of modes, f the frequency, V the volume of the cavity and c0 the speed of light in free space.
Following this criterion, we have chosen a cavity as large as possible, the only limits being the required space and the resulting weight. The final dimensions of our cavity are 2 m × 1 m × 1 m. However, to be representative of a real combustion chamber, which is much smaller, our cavity and the combustion chamber have to show the same electromagnetic behavior, i.e. the same number of modes. Following the equation of Weyl, this is reached if the product V * f3 is constant for both. For the real combustion chamber, this would mean an increase in frequency as the volume decreases, e.g. using a frequency of 20 GHz (factor 8) would reduce the dimensions of the cavity from meters to deci-meters, which corresponds to the order of magnitude of a real combustion chamber.
 |
Fig. 1 Electromagnetic cavity. |
2.2 The split ring resonator
2.2.1 Choice of the concentrator
The creation of a plasma in air at ambient pressure requires a high electric field and therefore a high microwave power density. The diffraction limit prohibits a wave to be focused into a sphere with a diameter smaller than λ/2. As a consequence, a plasma is more easily created when we increase the frequency. For the maximum frequency possible in our facility (3 GHz), the focal point is limited to a minimum diameter of 5 cm which makes it extremely difficult to reach the voltage for a plasma creation. One way to facilitate the plasma creation is to use concentrators that have often the form of tips. Unfortunately, with the power level we can create (2 kW), the peak effect of the tips is not it not sufficient to reach the breakdown threshold. Therefore, we have chosen a Split Ring Resonator (SRR) that, excited at its resonance frequency, has a highly increased electric field in its gap.
The geometry of a SRR is shown in Figure 2, with r the inner radius of the ring, h the height, w the width and g the gap. The SRR can be represented by a RCL equivalent circuit, where the ring is one loop of a coil (L), the gap is the capacitor (C) and R is the resistance that models the SRR’s electrical and radiation properties. To reduce this latter, we choose a ring made of copper. We are able to adjust the resonance frequency as a function of the geometrical parameters by using the classical equations in the literature [15]. As these equations are not exact, we conducted electromagnetic simulations with ANSYS HFSS. Figure 3 shows the resulting electric field in the middle plane of the SRR when excited at its resonance frequency fr . The magnetic field perpendicular to the loop of the SRR induces an electric current in the resonator. We can see that the electric field is highest (red color) in the gap. When the electric field is high enough in the gap, a plasma can be created.
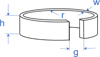 |
Fig. 2 SRR geometry. |
2.2.2 Dimensioning of the SRR
As the focus of the microwaves is better at higher frequencies, we chose to use the SRR at a frequency in the higher part of the bandwidth available with our material. We chose the geometric parameters of the SRR to reach a resonance frequency around 2.8 GHz. The parameter used are: r = 7mm, h = 1 mm, w = 1 mm and g = 1.6 mm. The simulation has confirmed the value of resonance frequency. However, the frequency value is very sensitive to the geometrical parameters and we chose to verify it experimentally. In order to do so, a set-up of two horn antennas facing each other in free space has been used. At first, the transmission coefficient has been measured between the two antennas in air. In a second step, a SRR has been placed between the two antennas to get the new transmission coefficient. Results are summarized in Figure 4. A distinct negative peak is measured in the case with SRR. It defines its resonance frequency fr , situated in the interval between 2.83 and 2.86 GHz. Around the resonance frequency, the SRR absorbs and radiates in all directions part of the incoming energy, therefore less energy is left to be transmitted between the horn antennas and the transmission coefficient decreases.
 |
Fig. 3 Simulation results of the electric field when SRR is excited at its resonance frequency. |
 |
Fig. 4 Measurements of the transmission coefficient to define the resonance frequency of the SRR. |
2.2.3 Configuration and placement of the SRR
To create a plasma in its gap, the SRR has to be installed at a position in the cavity where it will be excited by a magnetic field perpendicular to its axis at its resonance frequency fr . However, the distribution of the fields inside the cavity is governed by the electromagnetic modes. At a given frequency fc only a certain number of modes exists in the cavity associated to a specific distribution of field minima and maxima. By changing the frequency fc , the distribution of minima and maxima changes as well. Regarding the characteristics of the SRR and the cavity, we chose to install several SRR to maximize the chance that, at least, one of them is placed at a magnetic field maximum and therefore excited as we vary the frequency fc in the bandwidth of resonance (2.83–2.86 GHz). This is one of the conditions necessary for successful plasma creation (more details in the paragraph Remote Plasma Creation in SRRs). As the incoming power is split up between the SRRs, this is a compromise to fulfill these conditions and to increase the probablilty of plasma creation.
We chose to place 8 SRRs in a rectangular configuration, as shown in Figure 5. They are separated by a distance of 4 cm in each direction to limit electromagnetic coupling between them. To set up this configuration without disturbing their electromagnetic behavior, the SRR have been placed on glass wires (thin black lines in Fig. 5) that are stretched across a support in U-form (grey in Fig. 5). Every SRR is held by two wires and is oriented vertically with the gap facing the ceiling of the cavity to facilitate the ignition of a fuel spray (see paragraph on fuel injection system). This matrix of SRR has been installed in the cavity as shown in Figure 6, under the fuel injection system.
To verify that in the chosen frequency band the SRR are immerged by modes with the needed orientation of the magnetic field in the cavity, we have used a sensor next to the SRR matrix, as indicated in blue in Figure 5. This sensor is a magnetic loop, sensible to the magnetic field, oriented in the same direction as the SRRs. Connected to a Vector Network Analyzer (VNA) (Keysight, model no. E5071C), this sensor does not measure the absolute value of the magnetic field, but allows to quantify its variation. This way, we can see the variation of the magnetic field in the frequency range of 2.7–2.9 GHz, close to the SRR matrix, as shown in Figure 7. Every peak represents a mode. The diagram shows that in the resonance frequency range of 2.83–2.86 GHz, there are many modes in the cavity and therefore, the SRR will be excited as planned.
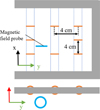 |
Fig. 5 SRRs configuration in the cavity (top and side views). |
2.3 Microwave power device
As shown in Figure 6, the monochromatic sinusoidal signal is created by a local oscillator (Agilent infiniium – model MSO9254A) which is amplified via a 2 kW pulsed microwave amplifier. We have to note that the pulsed function of the amplifier was not necessary for the experiments. The length of the impulsion used is of several microseconds and permits to consider the signal as sinusoidal during the time frame. The signal is then sent into the cavity via a power antenna. This antenna of a total length of 310 mm consists of a coaxial connector type N, a coaxial line and a solid copper cone connected to the inner conductor of the coaxial line at its extremity (see Fig. 8). This cone is used to ensure the emission of a large frequency band and to avoid a creation of plasma directly on the antenna due to the peak effect.
 |
Fig. 6 Scheme of the experimental set-up (top view). |
 |
Fig. 7 Transmission coefficient between the power antenna and the magnetic field probe in the interval of 2.7–2.9 GHz. |
 |
Fig. 8 Image of power antenna. |
2.4 Fuel injection system
For the liquid fuel, an ultrasonic injector (Sonics model USVC 130AT) with a cylindrical head has been used. A liquid film of kerosene is formed on its head and the excitation of the piezo-electric cell at 20 kHz promotes film instabilities, its subsequent break-up into ligaments and droplets, and the creation of a spray. This injector with a quasi-cylindrical spray, with a droplet Sauter mean diameter of the order of 50 µm and velocity of 1 m/s. Figure 9 presents the set-up for the ignition experiments. The position of the spray is shown under the form of a gray disc in the top view (Fig. 9). This gray area indicates the position of the liquid core of the spray. To ignite the fuel, it has to be evaporated and mixed with air. This ignitable mixture is formed around the core of the spray, in particular in the SRR region.
3 Results
3.1 Remote plasma creation in SRRs
To create a plasma in the gap of the SRR, we have to fulfill three conditions:
the operating microwave frequency has to match one or several modes of the cavity. (This point has been demonstrated in the previous paragraph with the VNA)
This frequency needs to be within the resonance frequency interval of the SRR (see paragraph ‘Dimensioning of the SRR’)
the SRRs have to be placed in a location where the magnetic field is high and perpendicular to their loop (see ‘Configuration and placement of the SRR’).
For the plasma creation experiments, we chose a frequency of 2.8467 GHz for which a maximum number of plasmas in the SRRs were created.
The magnetic field probe we put in the SRR array provides a visualisation of the signal arriving at its position for the two cases without and with plasma, as shown in Figures 10a and 10b.
Figure 10a shows the signal captured by the probe in the absence of plasma. After a short loading time of the cavity of 1 µs, the voltage measured reaches a more or less constant amplitude. In a second test, the incident power has been increased and the signal observed on the magnetic field probe is shown in Figure 10b. We can see again the loading time of the cavity, but then the amplitude decreases, while the incident signal has been kept constant. This behavior is associated to a plasma creation and the signal shows the electromagnetical signature of the presence of the plasma. In fact, the decrease of the voltage on the magnetic loop occurs because part of the power is absorbed by the plasma. This study was also helpful to define two key parameters to achieve plasma creation: the voltage threshold on the probe Vplasma and the time tplasma needed to load the cavity and for the SRR to create plasma. These parameters provide guidelines to realize the time reversal signal in future experiments. With this set-up, we have been able to successfully create a plasma on at least 4 SRRs in air at atmospheric conditions in a repeatable manner.
Figure 11 shows an example of a successful plasma creation with a pulsed microwave signal. The purple color is characteristic for an air plasma. The incident power for these experiments was Pinc ≈ 1600 W of which Prefl ≈ 100 W were reflected. This yields a power entering the cavity of Pcav ≈ Pinc − Prefl ≈ 1500 W.
 |
Fig. 9 Set-up for ignition experiments. Left: photo, center: top view of U support with SRRs, right: side view of the spray and U support only. |
 |
Fig. 10 (a) Signal captured by the magnetic field probe without plasma. (b) Signal captured by the magnetic field probe with plasma. |
 |
Fig. 11 Example of successful plasma creation in the SRR gaps. |
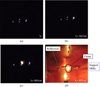 |
Fig. 12 Ignition sequence: (a) plasma creation, (b) ignition on the plasma far right, (c) ignition on the plasma in the middle, (d) propagation of flame to ignite the whole spray (mirrored flames can be seen on the copper surfaces). |
3.2 Fuel ignition
With regard to aeronautical application, ignition experiments of a kerosene spray in air with the microwave plasma system described above have been performed. The experiments follows a three-step process: 1. creation of the plasma; 2. injection of the liquid fuel during a defined time (automated spray sequence); 3. turn off of the microwave input and the plasma.
The spray sequence enables an automation and timing of the spray injection. The spray time tspray (during which the spray is injected) could be changed as necessary. For the presented results, we used a tspray = 2 s of a kerosene under a injection pressure of ≈2.7 bar and a mass flow of ≈1 kg/h.
The experiments have been filmed with two different cameras (IDS and smartphone). Figure 12 shows the ignition process of the kerosene spray. The ignition takes place at the position of the plasma, before the flame propagates to the bottom, following and burning the fuel that has already gone through the plasma. The flame propagates up again to reach and burn the incoming fuel. At the end of the experiment, the flame expands on the ceiling of the cavity, when the liquid fuel injection is turned off, before it extinguishes.
4 Discussion
The results have shown that a high power (Pcav of ≈1500 W) is needed to create the plasma and ignite the fuel spray. It has to be noted that this power fills the whole cavity (2 m3 volume) meaning that only a limited fraction of this power is located around the SRR matrix and is actually used for the plasma creation. With the planned application of the time reversal, we expect that this power can be drastically decreased, as the entering power can be focused spatially and temporally on the area of interest.
5 Conclusion and perspectives
In this paper we have presented a new, versatile cavity that can be used for various microwave applications. This cavity has been used to demonstrate the creation of plasma using SRRs with a remote microwave excitation in air at atmospheric conditions. In order to do so, a pulsed sinusoidal signal with a frequency of f = 2.8467 GHz has been injected into the cavity with a power Pcav of ≈1500 W. We proofed that the created plasma, although restricted to the gap zone, is energetic enough to evaporate and ignite a kerosene spray. These results showed the interest of this approach in the context of aeronautical ignition and will be used for further experiments, where we will test the plasma creation via a time reversal signal.
We thank the CEA Gramat for lending the microwave amplifier which made this work possible.
Conflict of interest
The authors have nothing to disclose.
Funding
This research work was funded by ONERA - The French Aerospace Lab and the Doctoral School 467 Aeronautics and Astronautics.
Data availability statement
My manuscript has data included as electronic supplementary material.
Author contribution statement
All the authors were involved in the preparation of the manuscript. All the authors have read and approved the final manuscript.
Supplementary Material
Supplementary Material provided by the author. Access here
References
- J.B. Michael, T.L. Chng, R.B. Miles, Combust. Flame 160, 796 (3) [Google Scholar]
- A.M.R.N. Alrashidi, Int. J. Energy Res. 42, 1813 (3) [Google Scholar]
- E.S. Stockman, S.H. Zaidi, R.B. Miles, C.D. Carter, M.D. Ryan, Combust. Flame 156, 1453 (3) [Google Scholar]
- A. Starikovskiy, N. Aleksandrov, Progr. Energy Combust. Sci. 39, 61 (3) [Google Scholar]
- S.M. Starikovskaia, J. Phys. D: Appl. Phys. 39, R265 (2006) [CrossRef] [Google Scholar]
- B. Done, Procedia Manuf. 22, 659 (3) [Google Scholar]
- S.A. O’Briant, Propuls. Power Res. 5, 1 (3) [Google Scholar]
- F. Auzas, Décharge radiofréquence produite dans les gaz à pression élevée pour le déclenchement de combustion, Ph.D. thesis, Paris 11, 2008 [Google Scholar]
- S. Lovascio, J. Hayashi, S. Stepanyan, G.D. Stancu, C.O. Laux, Proc. Combust. Inst. 37, 5553 (3) [Google Scholar]
- S. Bentaleb, Etude du déclenchement de combustion de mélanges air-propane et air-heptane par decharge mono- impulsionnelle nanoseconde, Ph.D. thesis, Université Paris Sud - Paris XI, 2012 [Google Scholar]
- M.K Le, A. Nishiyama, Y. Ikeda, Proc. Combust. Inst. 37, 5613 (3) [Google Scholar]
- A.M. Davydov, S.I. Gritsinin, I.A. Kossyi, Y.M. Shikhman, V.A. Vinogradov, IEEE Trans. Plasma Sci. 36, 2909 (3) [Google Scholar]
- M. Fink, Sci. Am. 281, 91 (3) [Google Scholar]
- V. Mazières, R. Pascaud, L. Liard, S. Dap, R. Clergereaux, O. Pascal, Appl. Phys. Lett. 115, 154101 (3) [Google Scholar]
- D.R Smith, J.B. Pendry, J. Opt. Soc. Am. B: Opt. Phys. 23, 391 (3) [Google Scholar]
- O. Sakai, S. Iio, Y. Nakamura, Plasma Fusion Res. 8, 1406167 (3) [Google Scholar]
- H. Kim, J. Hopwood, Sci. Rep. 9, 3024 (3) [Google Scholar]
- R. Navarro, L. Liard, J. Sokoloff, J. Appl. Phys. 126, 163304 (3) [Google Scholar]
- F. Iza, J.A. Hopwood, IEEE Trans. Plasma Sci. 31, 782 (3) [Google Scholar]
- R.A. Dextre, K.G. Xu, IEEE Trans. Plasma Sci. 45, 215 (3) [Google Scholar]
- P.K. Singh, J. Hopwood, S. Sonkusale, Sci. Rep. 4, 1 (3) [Google Scholar]
- D.A. Hill, Electromagnetic theory of reverberation chambers. (NIST Technical Note), 1998. [Google Scholar]
Cite this article as: Beatrice Fragge, Jérôme Sokoloff, Olivier Rouzaud, Olivier Pascal, and Mikael Orain, Fuel ignition using remote generation of microwave plasma in air at atmospheric pressure, Eur. Phys. J. Appl. Phys. 99, 2 (2024)
All Figures
 |
Fig. 1 Electromagnetic cavity. |
| In the text | |
 |
Fig. 2 SRR geometry. |
| In the text | |
 |
Fig. 3 Simulation results of the electric field when SRR is excited at its resonance frequency. |
| In the text | |
 |
Fig. 4 Measurements of the transmission coefficient to define the resonance frequency of the SRR. |
| In the text | |
 |
Fig. 5 SRRs configuration in the cavity (top and side views). |
| In the text | |
 |
Fig. 6 Scheme of the experimental set-up (top view). |
| In the text | |
 |
Fig. 7 Transmission coefficient between the power antenna and the magnetic field probe in the interval of 2.7–2.9 GHz. |
| In the text | |
 |
Fig. 8 Image of power antenna. |
| In the text | |
 |
Fig. 9 Set-up for ignition experiments. Left: photo, center: top view of U support with SRRs, right: side view of the spray and U support only. |
| In the text | |
 |
Fig. 10 (a) Signal captured by the magnetic field probe without plasma. (b) Signal captured by the magnetic field probe with plasma. |
| In the text | |
 |
Fig. 11 Example of successful plasma creation in the SRR gaps. |
| In the text | |
 |
Fig. 12 Ignition sequence: (a) plasma creation, (b) ignition on the plasma far right, (c) ignition on the plasma in the middle, (d) propagation of flame to ignite the whole spray (mirrored flames can be seen on the copper surfaces). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.