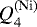EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 97 (2022) Eur. Phys. J. Appl. Phys., 97 (2022) 16 Full HTML
Issue
Eur. Phys. J. Appl. Phys.
Volume 97, 2022
Special Issue on ‘Nanoalloys: Kinetic and Environmental Behaviour’, edited by Pascal Andreazza, Riccardo Ferrando and Liu Xiaoxuan
Article Number 16
Number of page(s) 7
Section Physics of Organic Materials and Devices
DOI https://doi.org/10.1051/epjap/2021210246
Published online 10 March 2022

© F. Calvo, published by EDP Sciences, 2022

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

The interest in nanoalloys, or multimetallic nanoparticles, has grown substantially in the recent decades, motivated by the promise of newly emerging materials with unique and tunable properties [1,2]. Among the variety of metals that have been combined into nanoalloys, silver and nickel have been particularly scrutinized, owing to their potential interest in catalysis [3–8], energy production [9,10], optics [11] and even as nano inks [12]. As a result, their fundamental properties have been investigated in details as well, in particular their chemical reactivity [13], magnetism [14], or optical and plasmonic response [15–17].

Silver and nickel are characterized by a strong lattice mismatch causing them to be, at thermal equilibrium, essentially immiscible at all temperatures [18]. In the bulk limit, amorphous alloys can be obtained by cooling liquid mixtures fast enough, and for the Ag-Ni case heterogeneities were found to be nanometer large [19,20] with a strong icosahedral short-range order [21]. At the nanoscale and in vacuum, the lower surface energy of silver makes this element preferentially found at the surface, leading to morphologies of the Nicore@Agshell type, a feature that is clearly shown by computer simulations of the stable structures at the atomistic level of details [22–25], sometimes carried out using an explicit description of electronic structure [23,26–28], as well as continuum thermodynamical models of the Calphad type [29]. Atomistic simulations further showed how the internal strain can drive the nickel core away from the center of the nanoparticles [30]. Experimentally, Nicore@Agshell nanoparticle morphologies have been reported by a number of groups [16,31–33].

While the situation of silver-nickel nanoalloys at thermal equilibrium is reasonably well understood, out-of-equilibrium conditions are often desirable and met in experiments, where kinetic factors come into play and hinder the appearance of the Nicore@Agshell motif. Various groups have thus reported the successful synthesis of fully alloyed Ag-Ni nanoparticles through wet chemistry methods [14,17,34–38] but also by laser ablation [39], electrodeposition [40], radiolysis [41,42], ion implantation [43], or galvanic replacement [44]. Even the rather opposite structure with a silver core coated by a nickel shell, Agcore@Nishell, could be obtained on repeated occasions [45–49]. From the theoretical perspective, the onion-ring motif was shown to be yet another possible structure for silver-nickel nanoalloys grown atom by atom [50], and atomistic or kinetic studies over rather long time scales have been conducted as well [51,52].

In the present contribution, we further explore computationally the competition between kinetic and thermodynamic factors involved in the formation of silver-nickel nanoparticles, evolving from structures initially away from the expected equilibrium shape. By means of molecular dynamics (MD) simulations based on a classical many-body semiempirical potential, we find that phase separation between the two metals is a very robust feature, although the silver component exhibits a relatively weak tendency to aggregate. Extrapolations of specific properties allow us to provide crude relaxation times toward the expected core–shell equilibrium shape. Finally, silver impurities inside the nickel core are also produced upon annealing a hot vapor, but only occasionally, despite the fast cooling rates employed in our simulations, of the order of 109 K/s.

The article is organized as follows. In the next section we briefly describe the computational methodology and the MD protocol, especially the choice of initial conditions. We present and discuss the results in Section 3, before giving a few concluding remarks in Section 4.

2 Methodology

Our methodof choice relies on classical molecular dynamics simulations, using a many-body potential with parameters adapted to silver and nickel [50]. Because such potentials are semiempirical and adjusted to reproduce a limited number of reference data usually obtained at low temperatures, their accuracy and predictive capability are not expected to be as good as electronic structure methods such as density functional theory. However, they allow hundreds or thousands of atoms to be studied over time scales extending well beyond nanoseconds, both being our targetted ranges.

The details and parameters of the model can be found in the original work by Baletto and coworkers [50]. This model has since been used in a number of related studies [23,24,30,51–53] in which the stable structures but also kinetic effects were addressed.

The typical computational protocol implemented in the present work consists of annealing preexisting assemblies of Ag and Ni atoms, intwo possible ways that we denote as weakly and strongly out-of-equilibrium situations, respectively. In the weak case, the two metals are assumed to be already phase separated from the start, as sequential synthesis methods are capable of routinely producing, and only the silver part is purposedly imposed not to be a distinct, coating shell, but located either at the vertices of the nickel particle, or on its side in a Janus-like fashion, possibly as an independent nanoparticle. In the strong case, a completely mixed initial vapor of both elements is assumed to have been obtained by laser ablation from a bulk material, under vacuum conditions. The temperature imposed to these samples also depends on this nature, as it is set to 1200 K in the weak situation (essentially above the melting point of silver, but lower than the melting point of nickel), and 5000 K in the strongly out-of-equilibrium case. Temperature is controlled using a standard Nosé-Hoover thermostat and decreased stepwise.

Various properties are monitored as a function of time, depending also on the situation considered. The aggregation of silver atoms was measured based on a standard connectivity criterion (with a cut-off radius of 3 Å), and we have also determined the overall physical extension of the nanoparticles using the gyration tensor, extracting its first moment (gyration radius), as well as its second moment measuring the deviation to the spherical shape (dimensionless asphericity parameter χ) [54]. Chemical ordering and its time evolution were quantified using a mixing index μ defined as [24] 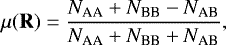(1)

where NXY denotes the number of nearest-neighbor bonds between atoms of types X and Y, as well as the conventional atom-specific radial distribution functions ρX(r), where r measures the distance between atoms and the center of the nanoparticle. The extent of crystalline character in the nickel part of the nanosystem was also determined using the bond-orientational order parameter Q4.

3 Results and discussion

3.1 Annealing of phase separated nanoparticles

We first consider two cases of moderate numbers of silver atoms deposited on preexisting nickel particles. Here the total number of atoms is fixed to be 923, corresponding to an ideal 6-shell icosahedron for a monatomic system. A first situation is that where the silver atoms are initially grown at the tips of the nickel solid core, as experimentally realized by Shviro and Zitoun [55]. Here the silver concentration is taken at 10%, and the silver atoms are initially substituted to nickel atoms from the corresponding perfect icosahedron.For comparison, we have also investigated the rather different starting point where all the silver initially forms a capping sideof the nanoparticle, in a Janus-like fashion, also with 10% silver, to assess the importance of initial configurations on the relaxation dynamics.

For both situations, the nanoparticles were subjected to annealing ramps ranging from 1200 K down to 400 K, by steps of decreasing 50 K every 12.5 ns. Figure 1 shows two specific properties as a double function of time (lower axes) and temperature (upper axes), namely the maximum size of the silver aggregate, and the mixing index μ defined in equation (1) above. The rearrangement of the silver atoms initially placed at the tips of the nickel icosahedron is relatively minor, although visual inspection clearly shows that most of them have migrated around, still forming a number of islands of various sizeson the nickel core, which incidentally has become more rounded upon annealing. The silver atoms do not exhibit preferential attachment to specific regions of the nickel surface. In the case where the silver atoms initially all cap the Janus particle into a single cluster, their significant mobility leads to the fragmentation of this cluster and the formation of several new islands, the largest of them being barely larger than when only 10% silver atoms were considered as previously. For the particle initially taken in the Janus configuration, the mixing index shows a major drop during the first 50 ns of annealing, which is associated to an increase of chemical mixing in the system as the single cluster progressively decays into several smaller fragments on the surface of the nickel core.

Similar simulations were performed for the larger nanoparticles containing 2869 atoms in total, or 9 equivalent shells for an ideal icosahedron, and at the silver concentration of 28% corresponding to the outer shell being of the other metal. In addition to such a core–shell system, the ideal Janus situation was also investigated for comparison with the previous case of a smaller nanoparticleat lower silver concentration. Owing to the size mismatch between silver and nickel, these initial configurations deviate quite sensitively from the perfect icosahedron assumed in the monometallic case (see insets of Fig. 2).

For these nanoparticles, which were computationally annealed following the same temperature protocol as used earlier for the 923-atom systems, the mixing index and size of the silver fragment are not very informative and were discarded from the analysis. Instead we have monitored the extent of local crystallinity in the nickel component using the Q4 bond-orientational order parameter, as well as the global shape of the entire nanoparticle through the asphericity parameter χ. The results, shown in Figure 2 as a double function of time and temperature, exhibits interesting differences between the two starting configurations. In the nanoparticle having its silver component initially at the surface (uniform outer layer of the icosahedron), the overal shape remains nearly spherical as the annealing proceeds, but the local order is markedly affected. In particular, while the crystalline content is initially very small due to the icosahedral nature of the particle (Q4 vanishingly low), it displays a very sharp increase when the silver layer has finished rearranging at the surface, at a temperature of about 950 K that corresponds to its freezing. The index Q4 that is being monitored here does not include the silver atoms, hence it is a signature of crystallization of the nickel part due to the migration of the silver layer.

Annealing the nanoparticle initially taken in an ideal Janus configuration (which due to the size mismatch looks more like an acorn), no such crystallization process is found in the nickel subpart, but the nanoparticle undergoes multiple deformation steps, becoming a much more spherical shape once the freezing temperature is reached. The most striking effect here is the fairly complete rearrangement of the initially capping silver subpart into a single atomic shell, the nickel core being also more rounded.

Although the analysis above relies on individual trajectories, the nanoparticle obtained by relaxing the core–shell symmetric structure is likely much closer to equilibrium than the one initially prepared in the Janus state. Local optimization of both products reveals that the latter is about 20 eV higher in energy than the former, thus showing that the surface rearrangement that involves mostly the silver atoms may be followed upon additional or longer annealing by a rearrangement of the nickel core.

A much more realistic Janus type configuration is that in which two separate nanoparticles from pure nickel and silver are placed in contact with each other, as produced independently from physical synthesis techniques. We have considered the natural evolution of such a nanosystem by imposing its temperature to two values below the melting point of silver, either 500 K or 1000 K. The influence of the more mobile silver atoms on the nickel subcluster was monitored by looking at its gyration radius 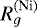, and the changes in chemical ordering through the mixing index μ. Both quantities are represented in Figure 3 together with pictures of the nanoparticles before and after thermal relaxation. As expected at such temperatures, the silver rearranges by coating the nickel cluster which is seeminglyless affected by the process. However, inspection of the nickel gyration radius clearly reveals that the nickel particle undergoes some general rounding, all the more than temperature is high, 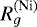decreasing by about 10% after 500 ns. Coating itself is better monitored on the mixing index μ, which necessarily decreases from the maximum value of μ = 1 obtained forthe fully separated nanoparticle with little contact between the two metals. As the interface between silver and nickel grows, more bonds are established between the two metals, although those never really mix, μ keeping a rather high positive value. The rate of variations in the mixing index is mostly steady after an initial strongly decreasing phase taking place over the first 20 ns approximately, and this indicates that the configurations extracted at 500 ns are still far from the equilibrium structures, in which the nickel core is expected to be fully coated by silver atoms.

In a first, very crude approximation, we can evaluate the time it would take to reach this equilibrium geometry, by extrapolating the linear variations in μ(t) to the time where μ reaches the value in the NicoreAgshell system. Taking the two examples depicted in Figure 2, we find very similar values for μ of 0.84 and 0.86, from which we only keep the average value of μ = 0.85 as a representative target in the equilibrium state. Linear extrapolation of the time-dependent numerical data after 200 ns leads to relaxation times of about 4.7 μs and 900 ns at 500 K and 1000 K, respectively.

thumbnail Fig. 1

Selected properties of a 923-atom Nicore@Agshell nanoparticle with 10% silver, initially allocated at the vertices of the icosahedral nickel core (shown as an inset in the upper panel), or forming a capping side in a Janus-like fashion (shown as an inset in the lower panel), as a function of increasing time and decreasing temperature: size of the largest silver cluster, and mixing index.
thumbnail Fig. 2

Selected properties of a 2869-atom Nicore@Agshell nanoparticlewith 28% silver, having its silver shell initially allocated as the outermost icosahedral shell over an icosahedral nickel core (shown as an inset in the upper panel), or forming a capping side in a Janus-like fashion (shown as an inset in the lower panel), as a function of increasing time and decreasing temperature: bond-orientational order parameter between nickel bonds, and asphericity parameter.
thumbnail Fig. 3

Selected properties of a 2869-atom Nicore@Agshell nanoparticlewith 28% silver, initially consisting of two pure nickel and silver nanoparticles in contact with each other, evolving at 500 K or 1000 K over 500 ns: gyration radius (upper panel) and mixing index (lower panel). The common initial structure, as well as the final structures at these two temperatures are shown as insets in the upper and lower panels, respectively, while the dashed lines emphasize the nearly linear time variations in the mixing index.

3.2 Annealing of a hot metallic vapor

After addressing rather mild rearrangements in already condensed nanoparticles, we now turn to the other extreme case of nanoparticles formed from the vapor phase, as relevant in laser ablation syntheses. Obviously, the many-body potential employed in the present computational work is not expected to be very realistic for describing the vapor phase (notably because the long-range interactions are not included explicitly in the model), hence we refrain from claiming any quantitative accuracy in its prediction: these simulations should be cautiously considered as exploratory.

Two types of annealing simulations were performed, keeping the silver concentration to be 10% but imposing 1000 or 2000 atoms in total at the beginning. For these simulations, a soft repulsive container with initial radius of 50 Å was also implemented in order to prevent irreversible evaporation especially at the high initial temperatures. Ten independent trajectories were performed for each system size, the resulting properties being obtained as simple arithmetic averages. For these simulations, the temperature was initially set to 5000 K and decreased by 200 K every 12.5 ns.

In Figure 4 we highlight the final half of the trajectories, illustrated on the two indices of the number of connected silver atoms, and mixing index μ, as a double function of increasing time and decreasing temperature. As was the case under mild annealing, the fraction of silver atoms struggles to form large clusters, the main fragment amounting to about 10–15 atoms once temperature has dropped to 500 K. Yet, this quantity essentially grows monotonically with decreasing temperature, indicating a steady growth, still without any complete phase separation into two well-defined subclusters of each metal.

The mixing index monotonically increases as well, with steps that are representative of the piecewise variations in the imposed temperature, and no significant size effect. This increase indicates that phase separation, although not complete, proceeds gradually with the progressive migration of silver atoms to form few, moderately large clusters. Visual depiction of the finally obtained structures (see insets of Fig. 4) suggests that a significant portion of these atoms lies at the surface, as expected from equilibrium thermodynamics arguments. However, it is useful to inspect the radial distribution functions for both elements, shown in Figure 5 after integrating the last piece of the annealing trajectory thermostatted at 500 K. The radial distribution for nickel is relatively smooth, with only minor oscillatory variations expected for a multi shell structure, resulting from a mostly spherical and amorphous nanoparticle. The Q4 index (not shown) remains below 0.05, confirming the absence of crystallinity. In contrast, the silver radial distribution is essentially localized as a single peak at the surface of the nickel core, which does not not necessarily imply that silver atoms are connected together. Yet several silver atoms remain stuck inside the nickel core, as highlighted on the graph and also in the inset of Figure 5, which displays one typical cross section of a nanoparticle. In average, 1–2silver atoms are stuck inside the nanoalloy at the size of 2000 atoms, and 0–1 atom in the smaller system.

Such a trapping of silver atoms is caused by the fast initial freezing associated with the overall condensation of the majority element (nickel) which also happens to be the metal with the higher melting point. It is a manifestation of kinetic stabilization already found in recent computational studies of nanoalloys and appears to be a rather general phenomenon occuring in miscible systems such as Ag-Au [56] but also in nonmiscible systems such as Fe-Au [57], as found for Ag-Ni here as well. Its seldom occurence in the smaller system only conveys that the nanoparticles must be large enough for the trapping of such impurities to be actually detectable. In even larger nanoparticles, we speculate that a partially alloyed core could be formed if the silver composition is sufficient, just as in the aforecited investigations.

However, while the formation of an alloyed core takes here the modest form of few localized impurities, we do not expect extended alloys because of the size mismatch between silver and nickel. In particular, further annealing the nanoparticles should make them relax towards the expected equilibrium structure of fully phase segregated core–shell structures. Clearly, the few hundreds of nanoseconds covered in the present molecular dynamics trajectories remain far too short, and kinetics still prevail in our case. A more complete investigation covering systematically, and altogether, the effects of size, composition, and cooling rate on the morphological diversity of the nanoparticles thus appears as a natural perspective of the present work.

thumbnail Fig. 4

Selected properties of 1000- and 2000-atom nanoparticles formed by condensation of an initially hot gas with 10% silver content, as a function of increasing time and decreasing temperature: size of the largest silver cluster and mixing index, averaged over 10 independent MD trajectories. Typical structures obtained at the end of the annealing process are shown in the insets of the upper (1000 atoms) and lower (2000 atoms) panels.
thumbnail Fig. 5

Unnormalized metal-resolved radial distribution functions of 1000- and 2000-atom nanoparticles formed by condensation of an initially hot gas with 10% silver content, at the final stage of the annealing process (500 K). The inset in the lower panel shows a cross section of one nanoparticle having silver impurities captured inside the nickel core, highlighted also in the silver radial distribution by dashed red lines.

4 Concluding remarks

In applied nanoscience, it can often be desirable to enforce metastable configurations that are driven by the kinetics of the specific synthesis method, rather than the long-time thermodynamics expectations. Metals that are fully immiscible in the bulk offer a particularly rich playground for such effects, as they can become partially or even fully miscible once at the nanoscale. In the present contribution, we explored along such lines the specific case of nickel-silver nanoparticles by means of atomistic modeling. Two limiting cases were considered, in which either mild or strong rearrangements in the atomic structure and chemical ordering were expected depending on the initial conditions chosen in the simulations.

The relaxation towards the expected equilibrium shape of NicoreAgshell particles was first addressed by imposing symmetrically distributed silver atoms around an icosahedral nickel core, or a Janus-type allocation on one capping side, possibly under the form of two distinct nanoparticles in mere contact with one another. In all cases the silver atoms first spread over the nickel core, altering its shape and, possibly later on, its crystallinity, silver showing only limited propensity for surface aggregation at low concentration. In the more extreme case of annealing a hot vapor mixture, the finally obtained nanoparticles clearly exhibit the expected NicoreAgshell motif but with silver impurities as the main imperfection.

These results encourage us to explore the relationship between the synthesis protocol, the initial structure, the size and the composition of the particles and the annealing conditions in deeper details. In particular, it would be of great interest to identify the important physical parameters driving an initially hot vapor into any of the important morphologies known to exist experimentally such as core–shell, alloyed, onion-ring, and the numerous variations among those. A more systematic investigation of the true kinetic pathways between the various structural motifs, possibly carried in the rigorous framework of transition path sampling [58], would provide a more complete statistical view of the underlying rearrangement mechanisms. In addition, such an analysis would benefit of machine learning tools that have become now widespread in materials science, especially for classification problems.

Supplementary Material

Movies showing the structural rearrangement for nanoparticles analysed in Figures 1–3, in mp4 video format. Access here

References

  1. R. Ferrando, J. Jellinek, R.L. Johnston, Chem. Rev. 108, 845 (2008) [CrossRef] [PubMed] [Google Scholar]
  2. F. Calvo (ed) Nanoalloys: from fundamentals to emerging applications, 2nd edn. (Elsevier, Amsterdam, 2020) [Google Scholar]
  3. M. Kumar, S. Deka, ACS Appl. Mat. Interfaces 6, 16071 (2014) [CrossRef] [PubMed] [Google Scholar]
  4. M.H. Tang, C. Hahn, A.J. Klobuchar, J.W. Desmond Ng, J. Wellendorff, T. Bligaard, T.F. Jaramillo, Phys. Chem. Chem. Phys. 16, 19250 (2014) [CrossRef] [PubMed] [Google Scholar]
  5. R. Dhanda, M. Kidwai, J. Mat. Chem. A 3, 19563 (2015) [CrossRef] [Google Scholar]
  6. C.S. Budi, J.R. Deka, D. Saikia, H.-M. Kao, Y.-C. Yang, J. Hazard. Mater. 384, 121270 (2019) [Google Scholar]
  7. B. Yu, T. Ayavl"i", E. Raine, T. Li, M.M.-J. Li, J. Zheng, S. Wu, A.A. Bagabas, S.C.E. Tsang, Appl. Catal., B 243, 304 (2019) [CrossRef] [Google Scholar]
  8. S. Ghosh, A.K. Tiwari, Surf. Sci. 701, 121695 (2020) [CrossRef] [Google Scholar]
  9. M. Chandel, P. Makkar, N.N. Ghosh, ACS Appl. Electrochem. Mater. 1, 1215 (2019) [CrossRef] [Google Scholar]
  10. R. Majee, A. Kumar, T. Das, S. Chakraborty, S. Bhattacharyya, Angew. Chem. Int. Ed. 59, 2881 (2020) [CrossRef] [PubMed] [Google Scholar]
  11. K. Sridharan, T. Endo, S.-G. Cho, J. Kim, T.J. Park, R. Philip, Optical Mat. 35, 860 (2013) [CrossRef] [Google Scholar]
  12. M.M. Mohammadi, S.S. Gunturi, S. Shao, S. Konda, R.D. Buchner, M.T. Swihart, Chem. Eng. J. 372, 648 (2019) [CrossRef] [Google Scholar]
  13. A. Rossi, M. Zannotti, M. Cuccioloni, M. Minicucci, L. Peletta, M. Angeletti, R. Giovannetti, Nanomaterials 11, 1733 (2021) [CrossRef] [PubMed] [Google Scholar]
  14. K. Santhi, E. Thirumal, S.N. Karthick, H.-J. Kim, M. Nidhin, V. Narayanan, A. Stephen, J. Nanopart. Res. 14, 868 (2012) [CrossRef] [Google Scholar]
  15. M. Gaudry, E. Cottancin, M. Pellarin, J. Lerme, L. Arnaud, J.R. Huntzinger, J.L. Vialle, M. Broyer, J.L. Rousset, M. Treilleux, P. Melinon, Phys. Rev. B 67, 155409 (2003) [CrossRef] [Google Scholar]
  16. E. Cottancin, M. Gaudry, M. Pellarin, J. Lerme, L. Arnaud, J.R. Huntzinger, J.L. Vialle, M. Treilleux, P. Melinon, J.-L. Rousset, M. Broyer, Eur. Phys. J. D 24, 111 (2003) [CrossRef] [Google Scholar]
  17. R. Udayabhaskar, P. Sreekanth, B. Karthikeyan, Plasmonics 11, 1461 (2016) [CrossRef] [Google Scholar]
  18. M. Singleton, P. Nash, Bull. Alloy Phase Diag. 8, 119 (1987) [CrossRef] [Google Scholar]
  19. J.H. He, H.W. Sheng, P.J. Schilling, C.-L. Chien, E. Ma, Phys. Rev. Lett. 86, 2826 (2001) [CrossRef] [PubMed] [Google Scholar]
  20. J.H. He, E. Ma, Phys. Rev. B 64, 144206 (2001) [CrossRef] [Google Scholar]
  21. W.K. Luo, H.W. Scheng, F.M. Alamgir, J.M. Bai, J.H. He, E. Ma, Phys. Rev. Lett. 92, 145502 (2004) [CrossRef] [PubMed] [Google Scholar]
  22. F. Baletto, C. Mottet, A. Rapallo, G. Rossi, R. Ferrando, Surf. Sci. 566, 192 (2004) [CrossRef] [Google Scholar]
  23. A. Rapallo, G. Rossi, R. Ferrando, A. Fortunelli, B.C. Curley, L.D Lloyd, G.M. Tarbuck, R.L. Johnston, J. Chem. Phys. 122, 194308 (2005) [CrossRef] [PubMed] [Google Scholar]
  24. F. Calvo, E. Cottancin, M. Broyer, Phys. Rev. B 77, 121406(R) (2008) [CrossRef] [Google Scholar]
  25. M. Molayem, V.G. Grigoryan, M. Springborg, J. Phys. Chem. C 115, 7179 (2011) [CrossRef] [Google Scholar]
  26. M. Harb, F. Rabilloud, D. Simon, Chem. Phys. Lett. 449, 38 (2007) [CrossRef] [Google Scholar]
  27. S. Datta, A.K. Raychaudhuri, T. Saha-Dasgupta, J. Chem. Phys. 146, 164301 (2017) [CrossRef] [PubMed] [Google Scholar]
  28. R.H. Aguilera-del-Toro, P.G. Alvarado-Leyva, A. Vega, J. Magn. Magn. Mater. 474, 551 (2019) [CrossRef] [Google Scholar]
  29. Z. Zhao, F.-H. Wang, A. Fisher, Y. Shen, D. Cheng, J. Alloys Compd. 708, 1150 (2017) [CrossRef] [Google Scholar]
  30. D. Bochicchio, R. Ferrando, Nano Lett. 10, 4211 (2010) [CrossRef] [PubMed] [Google Scholar]
  31. L. Chung-Che, C. Dong-Hwang, Nanotechnology 17, 3094 (2006) [CrossRef] [Google Scholar]
  32. L. Kabir, A.R. Mandal, S.K. Mandal, J. Magn. Magn. Mater. 322, 934 (2010) [CrossRef] [Google Scholar]
  33. S.T. Park, T.-H. Kim, D.-W. Park, Appl. Surf. Sci. 374, 257 (2016) [CrossRef] [Google Scholar]
  34. S. Yan, D. Sun, Y. Tan, X. Xing, H. Yu, Z. Wu, J. Phys. Chem. Solids 98, 107 (2016) [CrossRef] [Google Scholar]
  35. S.S. Alruqi, S.A. Al-Thabaiti, M.A. Malik, Z. Khan, Colloids Surf., A 540, 36 (2018) [CrossRef] [Google Scholar]
  36. H.-H. Zhou, Y.-L. Li, J.-Q. Huang, C.-X. Fang, D. Shan, Y.-F. Kuang, Trans. Nonferrous Mat. Soc. China 25, 4001 (2015) [CrossRef] [Google Scholar]
  37. C. Srivastava, S. Chithra, K.D. Malviya, S.K. Sinha, K. Chattopadhyay, Acta Mater. 59, 6501 (2011) [CrossRef] [Google Scholar]
  38. S. Tabatabaei, S.K. Sadrnezhaad, Bull. Mater. Sci. 37, 1447 (2014) [CrossRef] [Google Scholar]
  39. Q. Xiao, Z. Yao, J. Liu, R. Hai, H.Y. Oderji, H. Ding, Thin Solid Films 519, 7116 (2011) [CrossRef] [Google Scholar]
  40. B.M. Mundotiya, C. Srivastava, Electrochem. Solid-State Lett. 15, K41 (2012) [CrossRef] [Google Scholar]
  41. Z. Zhang, T.M. Nenoff, J.Y. Huang, D.T. Berry, P.P. Provencio, J. Phys. Chem. C 113, 1155 (2009) [CrossRef] [Google Scholar]
  42. Z. Zhang, T.M. Nenoff, K. Leung, S.R. Ferreira, J.Y. Huang, D.T. Berry, P.P. Provencio, R. Stumpf, J. Phys. Chem. C 114, 14309 (2010) [CrossRef] [Google Scholar]
  43. Y. Shen, Y. Qiao, T. Jin, S. Yu, Z. He, Mat. Lett. 15, 1 (2015) [CrossRef] [Google Scholar]
  44. N.G. Gaidhani, S. Patra, H.S. Chandwadkar, D. Sen, C. Majumder, S.V. Ramagiri, J.R. Bellare, Langmuir 37, 1637 (2021) [CrossRef] [PubMed] [Google Scholar]
  45. M. Tsuji, S. Hikino, M. Matsunaga, Y .Sano, T. Hashizume, H. Kawazumi, Mat. Lett. 64, 1793 (2010) [CrossRef] [Google Scholar]
  46. L. Xia, X. Hu, H. Zhao, M. Sun, X. Cihen, Colloids Surf. A 367, 96 (2010) [CrossRef] [Google Scholar]
  47. G. Huizhang, C. Yuanzhi, C. Xiaozhen, W. Ruitao, Y. Guang-Hui, P. Dong-Liang, Nanotechnology 22, 195604 (2011) [CrossRef] [PubMed] [Google Scholar]
  48. J. Pinkas, J. Sopousšek, P. Brož, V. Vykoukal, J. Buršik, J. Vřešt́ál, Calphad 64, 139 (2019) [CrossRef] [Google Scholar]
  49. V. Vykoukal, J. Bursik, P. Roupcova, D.A. Cullen, J. Pinkas, J. Alloys Compd. 770, 377 (2019) [CrossRef] [Google Scholar]
  50. F. Baletto, C. Mottet, R. Ferrando, Phys. Rev. Lett. 90, 135504 (2003) [CrossRef] [PubMed] [Google Scholar]
  51. F. Calvo, A. Fortunelli, D.J. Wales, J. Chem. Phys. 139, 111102 (2013) [CrossRef] [PubMed] [Google Scholar]
  52. D. Nelli, R. Ferrando, Nanoscale 11, 13040 (2019) [CrossRef] [PubMed] [Google Scholar]
  53. E. Panizon, R. Ferrando, Nanoscale 8, 15911 (2016) [CrossRef] [PubMed] [Google Scholar]
  54. M. Bonnin, C. Falvo, F. Calvo, T. Pino, P. Parneix, Phys. Rev. A 99, 042504 (2019) [NASA ADS] [CrossRef] [Google Scholar]
  55. M. Shviro, D. Zitoun, J. Phys. Chem. C 118, 10455 (2014) [CrossRef] [Google Scholar]
  56. T.W. Liao, A. Yadav, K.J. Hu, J. van der Tol, S. Cojensino, F. D’Acapito, R.E. Palmer, C. Lenardi, R. Ferrando, D. Grandjean, et al., Nanoscale 10, 6684 (2018) [CrossRef] [PubMed] [Google Scholar]
  57. J. Johny, O. Prymak, M. Kamp, F. Calvo, S.-H. Kim, A. Tymoczko, A. El-Zoka, C. Rehbock, U. Schürmann, B. Gault, L. Kienle, S. Barcikowski, Nano Res. (2021) doi: 10.1007/s12274-021-3524-7 [Google Scholar]
  58. C. Dellago, P.G. Bolhuis, F.S. Csajka, D. Chandler, J. Chem. Phys. 108, 1964 (1998) [CrossRef] [Google Scholar]

Cite this article as: Florent Calvo, Structural relaxation in Ag-Ni nanoparticles: atomistic modeling away from equilibrium, Eur. Phys. J. Appl. Phys. 97, 16 (2022)

All Figures

thumbnail Fig. 1

Selected properties of a 923-atom Nicore@Agshell nanoparticle with 10% silver, initially allocated at the vertices of the icosahedral nickel core (shown as an inset in the upper panel), or forming a capping side in a Janus-like fashion (shown as an inset in the lower panel), as a function of increasing time and decreasing temperature: size of the largest silver cluster, and mixing index.
In the text
thumbnail Fig. 2

Selected properties of a 2869-atom Nicore@Agshell nanoparticlewith 28% silver, having its silver shell initially allocated as the outermost icosahedral shell over an icosahedral nickel core (shown as an inset in the upper panel), or forming a capping side in a Janus-like fashion (shown as an inset in the lower panel), as a function of increasing time and decreasing temperature: bond-orientational order parameter between nickel bonds, and asphericity parameter.
In the text
thumbnail Fig. 3

Selected properties of a 2869-atom Nicore@Agshell nanoparticlewith 28% silver, initially consisting of two pure nickel and silver nanoparticles in contact with each other, evolving at 500 K or 1000 K over 500 ns: gyration radius (upper panel) and mixing index (lower panel). The common initial structure, as well as the final structures at these two temperatures are shown as insets in the upper and lower panels, respectively, while the dashed lines emphasize the nearly linear time variations in the mixing index.
In the text
thumbnail Fig. 4

Selected properties of 1000- and 2000-atom nanoparticles formed by condensation of an initially hot gas with 10% silver content, as a function of increasing time and decreasing temperature: size of the largest silver cluster and mixing index, averaged over 10 independent MD trajectories. Typical structures obtained at the end of the annealing process are shown in the insets of the upper (1000 atoms) and lower (2000 atoms) panels.
In the text
thumbnail Fig. 5

Unnormalized metal-resolved radial distribution functions of 1000- and 2000-atom nanoparticles formed by condensation of an initially hot gas with 10% silver content, at the final stage of the annealing process (500 K). The inset in the lower panel shows a cross section of one nanoparticle having silver impurities captured inside the nickel core, highlighted also in the silver radial distribution by dashed red lines.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.