| Issue |
Eur. Phys. J. AP
Volume 2, Number 2, May 1998
|
|
|---|---|---|
| Page(s) | 175 - 181 | |
| DOI | https://doi.org/10.1051/epjap:1998170 | |
| Published online | 15 May 1998 | |
https://doi.org/10.1051/epjap:1998170
Rheological modelling of complex fluids: II. Shear thickening behavior due to shear induced flocculation
Laboratoire de Biorhéologie et d'Hydrodynamique
Physico-chimique,
LBHP, case 7056, Université Denis Diderot (Paris 7) (CNRS URA 443),
2 place Jussieu, 75251 Paris Cedex 05, France
Received:
27
November
1997
Accepted:
5
March
1998
Published online: 15 May 1998
The structural model discussed in Part I of the present
work is applied to "true" behavior – i.e. shear thinning
followed by shear thickening (sometimes followed by shear thinning) –
very often observed in complex fluids as
the applied shear is increased. This model states
that the viscosity η of these fluids – described as concentrated
dispersions of several classes of Structural Units (SUs) – is a unique
function of a flow-dependent effective
volume fraction, φeff. The latter is expressed in terms of
Si = fraction of "aggregated" particles contained in all
the SUis (as SUs of i-class) and Ci = (ϕi−1−1)=
"compactness factor", directly related to the mean
compactness ϕi of SUis.
Shear induced flocculation (SIF) is the more obvious
process capable to explain the shear thickening
behavior of partially flocculated suspensions (obviously,
another process should be required for stabilized
dispersions). After progressive reduction of SUs submitted
to shear forces (i.e. leading to a decrease of Si), such
a behavior should be observed if SIF
occurs beyond a critical shear rate 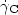 ,
then resulting in re-increase of Si,
thus of φeff and η. The simplest "SIF-model" will
introduce only one class of SUs, with only one variable S
governed by a kinetic equation in which the kinetic rate
for SU-formation increases with shear, thus giving the
expected shear-thickening behavior if
,
then resulting in re-increase of Si,
thus of φeff and η. The simplest "SIF-model" will
introduce only one class of SUs, with only one variable S
governed by a kinetic equation in which the kinetic rate
for SU-formation increases with shear, thus giving the
expected shear-thickening behavior if  .
However, at high shear rates, SIF is limited by a (Smoluchowski-like)
shear decreasing sticking probability. Effects of varying
model parameters on predictions of the resulting
SIF-model are discussed. Finally, this model is tested by
comparison with observed rheological behavior, namely
viscosity change vs. pH in aqueous styrene-ethylacrylate
dispersions, from Laun's data [2].
.
However, at high shear rates, SIF is limited by a (Smoluchowski-like)
shear decreasing sticking probability. Effects of varying
model parameters on predictions of the resulting
SIF-model are discussed. Finally, this model is tested by
comparison with observed rheological behavior, namely
viscosity change vs. pH in aqueous styrene-ethylacrylate
dispersions, from Laun's data [2].
PACS: 82.70.-y – Disperse systems / 83.20.Bg – Macroscopic (phenomenological) theories / 83.50.Ax – Steady shear flows
© EDP Sciences, 1998
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


