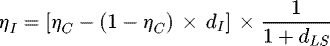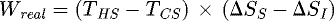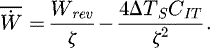| Issue |
Eur. Phys. J. Appl. Phys.
Volume 94, Number 3, June 2021
|
|
|---|---|---|
| Article Number | 30901 | |
| Number of page(s) | 6 | |
| Section | Physics of Energy Transfer, Conversion and Storage | |
| DOI | https://doi.org/10.1051/epjap/2021200390 | |
| Published online | 21 June 2021 | |
https://doi.org/10.1051/epjap/2021200390
Regular Article
Endo-irreversible thermo-mechanical Carnot engine with new concept of entropy production action coefficient
1
Université de Lorraine, CNRS, LEMTA, Nancy F-54000, France
2
SAS INVIVO Consulting, Nantes F-44000, France
* e-mail: michel.feidt@univ-lorraine.fr
Received:
30
December
2020
Received in final form:
28
March
2021
Accepted:
21
May
2021
Published online: 21 June 2021
Thermostatics of Carnot engines has been extended by more recent research based on endo-reversible model. Our model assumes exo-reversibility but endo-irreversibility to determine new upper-bound to thermomechanical conversion. We propose a functional expression of entropy production related to cycle transformation durations. This approach analyses the energy, entropy and power consequences. We introduce a new concept of entropy production actions that results in three sequential optimums: maximum energy related to transformation durations, maximum energy associated with equipartition of entropy actions, optimal power for given cycle period.
Note to the reader: Further to the publication of an erratum, the citation of the article was modified on 19 July 2021.
© M. Feidt and R. Feidt, Published by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The industrial revolution took off in conjunction with that of Thermodynamics. While the engineer's concerns were important, the fact remains that more fundamental research has accompanied the development of thermal engines (or more precisely thermo-mechanics).
Under the probable influence of his father L. Carnot who was a scientist and a mathematician [1], S. Carnot was the first to make the link between mechanics and thermal science [2] in a determining contribution that makes him one of the founding fathers of the Equilibrium Thermodynamics. He is thus credited with several decisive contributions [3]:
-
the notion of thermodynamic cycle, including the cycle that bears its name.
-
the extension of the notion of mechanical efficiency, to the efficiency of a thermomechanical engine (we now say internal efficiency in the sense of the first law of thermodynamics, ηI), adimensional form of efficiency.
S. Carnot has shown that this efficiency is an upper bound that is called, the Carnot efficiency, ηC. This efficiency characterize the two heat reservoirs engines, operating almost statically (Thermodynamics of equilibrium, T.E.). Assuming the isothermal source at THS (thermostat), as well as the isothermal sink at TCS < THS, he obtains: (1)
(1)
TCS, cold sink temperature; THS, hot source temperature.
Since then, numerous studies have been carried out on the Carnot cycle, or the Carnot engines (268 references with these keywords have been recorded for the last 3 years). The scope of this list goes far beyond engineering and classical physics, to quantum, molecular, photonic motors… Other models leave the small scales (nano-physics) to consider large structures (especially black holes), or life.
For this proposal, we will continue to focus on the phenomenological approach of classical thermodynamics at mesoscopic (human) scales.
In this context, there is a revival of work aimed at considering the influence of out-of-balance cycles transformations. The article most often cited as marking this revival is the 1975 article by Curzon-Ahlborn [4]. In fact, as we have shown [5], this work was preceded by other work in 1957 [6,7] and even before [8].
The majority of these works assumes temperature differences between the hot source and the engine (possibly between the engine and the sink), but in the end, considers an endo-reversible engine (without internal irreversibility) for optimization.
In addition, the optimization focuses on 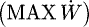 maximum power (in watt) of the engine. The choice of this objective function is logical, since it is the useful effect of an engine. Nevertheless, some details will be added in this article. The key result of the optimization is the demonstration of the engine's performance at maximum power:
maximum power (in watt) of the engine. The choice of this objective function is logical, since it is the useful effect of an engine. Nevertheless, some details will be added in this article. The key result of the optimization is the demonstration of the engine's performance at maximum power: (2)
(2)
This efficiency is much lower than the efficiency of Carnot, but the engine provides a given power (which is not the case for the Equilibrium Thermodynamics model). Since then, research has shown that the relationship (2) is not generic [9–11]. This article essentially proposes two things:
-
unlike the majority of proposals that focus on external heat transfers irreversibilities, we develop the case where heat transfers are perfect (exo-reversibility), but where the internal irreversibilities of the converter are taken into account whatever they are. Low dissipation models [11] or pseudo-cycles of Carnot [12] are not used. Then the importance of heat transfer entropies appears (see Sect. 2).
-
we will consider 2 major cases of optimization: either in W energy or in average power
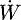 (and not instantaneous power, as we will justify (see Sect. 3).
(and not instantaneous power, as we will justify (see Sect. 3). -
in these cases, the influence of the form of internal irreversibilities will be particularly studied, as well as the consequences resulting from it.
Section 4 will be dedicated to the discussion and synthesis of the results. The resulting perspectives will be proposed.
2 Endo-irreversible model for Carnot engine
Unlike the vast majority of articles on the subject, we present a model whose irreversibilities are internal to the converter and represented globally, as will be seen below. Section 3 is relative to power optimization contrary to Section 2 concerned by energy optimization.
2.1 Models with thermal losses
However, to be complete, Figure 1 shows the Carnot engine between the hot thermostat at THS and the cold thermostat at TCS. It is noted that this diagram incorporates the presence of thermal losses (through the material structure) between the warmest point and the coldest point. The heat loss conductance equivalent to the KLS system typically leads, assuming linear heat transfers, to the expression of the lost heat energy QLS (J): (3)
(3)
ζ, operating time to be specified (s).
KLS, average conductance of heat losses over the operating time (W/K).
Generally speaking, the following will be written: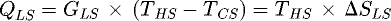 (4)
(4)
GLS, energy conductance of thermal losses (J.K−1)
ΔSLS, heat loss transfer entropy, (J.K−1) at the source during ζ.
To preserve generality as much as possible, we will keep the QHS energy expenditure in the form of: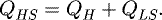 (5)
(5)
By posing QH = THS × ΔSH, as well as QC = TCS × ΔSC,we get: (6)
(6)
The entropy balance to the converter is written over the same period: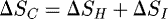 (7)
(7)
ΔSI, internal entropy production of converter during ζ.
We deduce, the mechanical work produced over the same period, using the energy balance of the converter by difference of heat at the hot source, then at the cold sink of the engine (QH − QC):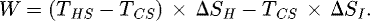 (8)
(8)
We find here that the maximum mechanical energy is obtained when the production of entropy is cancelled (totally reversible cycle). But we note that this energy depends on the thermal potential ΔTS = THS − T0, and also on the converted entropy of heat transfer between hot thermostat and converter, which we will take as reference ΔSH = ΔS.
The expression of performance in the sense of the first law of thermodynamics is then expressed by: (9)
(9)
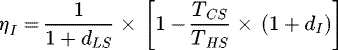 (9 bis)
(9 bis)
with dI, degree of irreversibility of the converter = 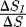
dLS, degree of thermal loss (for the system including source and sink) =  .
.
The expression (9) shows that heat losses introduce a reduction in efficiency related to the ratio dLS (usually in the order of a few percent). Similarly, internal irreversibilities attenuate the efficiency through dI, but weighted by the factor 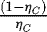 as can be seen on (9ter). Engines with a small temperature difference are therefore penalized.
as can be seen on (9ter). Engines with a small temperature difference are therefore penalized.
Moreover, the existence of a source temperature threshold leading to a performance that is physically acceptable to the engine can be observed with a fixed degree of irreversibility: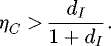
In general, dI is less than 1.
Or at given temperatures, the existence of an irreversibility threshold: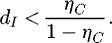
The study related to the degree of thermal loss of the system only makes sense for a heat thermostat of finite energy Q0. It is then easy to show that: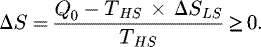 (10)
(10)
This leads to either a condition on ΔS (10bis)
(10bis)
Either on a condition of Q0
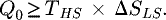 (10ter)
(10ter)
But the relationship (10) also shows the existence of a maximum temperature achievable for a finite energy source, or temperature of stagnation TS (common concept in solar energy)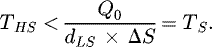 (11)
(11)
This relationship can also be interpreted in 2 other forms: (11bis) or
(11bis) or
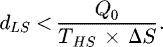 (11ter)
(11ter)
They induce, at THS temperature and source energy imposed, either a limitation of transfer entropy to the converter, or a limitation of the degree of thermal losses.
In the following paragraph, we will assume for simplicity, an endo-irreversible Carnot engine without thermal losses.
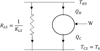 |
Fig. 1 General schematic representation of the endo-irreversible Carnot engine with thermal losses. |
2.2 Endo-irreversible Carnot engine model
The endo-irreversible Carnot cycle is shown in Figure 2. It typically consists of four transformations: 2 isotherms and 2 irreversible adiabatics. The fully reversible cycle is shown in Figure 2 as cycle 1 rev − 2 rev − 3 rev − 4 rev. It corresponds to the input of the converter QH rev as: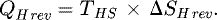
For this same reversible cycle, but at the cold end, we obtain: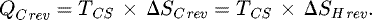
The mechanical energy in the reversible case is then expressed in the form: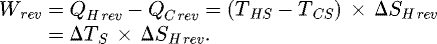 (12)
(12)
For the sake of simplification, the following are provided (see Fig. 2):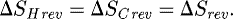
For the endo-irreversible cycle, at each transformation a production of entropy is associated: ΔSIH for the high temperature isotherm; ΔSIEx for the adiabatic expansion; ΔSIC for the low temperature isotherm; ΔSIC0 for the adiabatic compression.
Each transformation degrades mechanical energy = area 1 for the high temperature isotherm; area 2 for the adiabatic expansion, area 3 for the low temperature isotherm; area 4 for the adiabatic compression. Therefore, the mechanical work of the endo-irreversible cycle corresponds to area 1-2-3-4: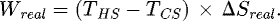
However, the entropic balance of the cycle (S, state function) provides: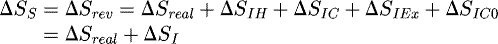
ΔSS, heat transfer entropy available at the source in the reversible case, or total entropy of the system (source + converter + sink)
ΔSI, total entropy production of the cycle.
ΔSreal actually, corresponds to conversion entropy. We deduce the expression of the efficiency of the endo-irreversible motor in relation to the heat transfer entropy of the reversible case ΔSS = ΔSrev: (14)
(14)
with  , the degree of irreversibility of the converter (introduced by I. Novikov) [7].
, the degree of irreversibility of the converter (introduced by I. Novikov) [7].
The reversible limit (dI = 0) well restores the Carnot efficiency of the equilibrium Thermodynamics, according to a more coherent scheme than the one proposed by Wang and He [12] and conforming to previous definitions [13].
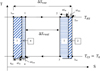 |
Fig. 2 Representation of the reversible and endo-irreversible Carnot cycles, in the diagram (T, S). |
2.3 Finite-time optimization of engine energy
We will assume here that the 4 transformations of the cycle are done in finite time, according to the schema similar to those used in some works including [12]. It is thus assumed that each transformation takes place in a duration ζi, but with a finite total duration ζ imposed for the cycle such that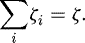 (15)
(15)
The simplest hypothesis for dissipations is, whatever the transformation, to assume them inversely proportional to ζi: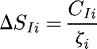 (16)
(16)
with CIi irreversibility coefficients [J.s/K].
Indeed, this hypothesis well restores the quasi-static limit of the equilibrium Thermodynamics when ζi→ ∞. It should be noted that the CIi irreversibility coefficients are positive finite quantities, having the dimension [J.s/K]. We call them entropy production action (a new concept analogous to energy action).
The combination of (13, 16) and the use of constraint (15) lead by using the variational calculation to the optimization of the transformation times of the cycle in relation to the mechanical energy produced: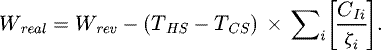 (17)
(17)
And to the following Lagrangian: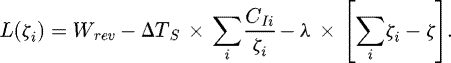 (18)
(18)
Hence, the expression of the corresponding maximum energy (first sequential optimum):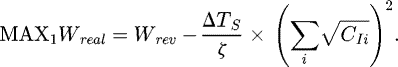 (19)
(19)
It is to be noted that this result is more general than the mechanical energy ;it is valid for all kinds of energy forms excepted the thermal energy only concerned by source and sink and efficiency at maximum energy output becomes: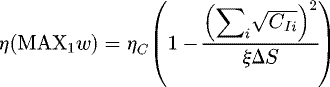 (20)
(20)
with ξΔS, cycle entropic transfer action.
2.4 Case where the entropic action is a finite physical dimension
We have shown in paragraph 2.3 that the maximum mechanical energy is associated with an optimal distribution of the durations of each transformation of the cycle, as long as the total duration (or cycle period) is fixed (finite time constraint).
This first maximum in energy (19) appears as a function of the entropic actions of each thermodynamic transformation. By imposing that entropic actions are also a finite physical dimension such as: (21)
(21)
The optimization by the variational calculation then leads to the equipartition of the entropic actions of each transformation: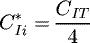 (22)
(22)
CIT, total entropic action distributed optimally over the cycle. It corresponds to the second maximum of energy MAX2Wreal, obtained sequentially: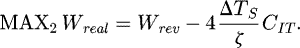 (23)
(23)
The conclusion of the previous optimization calculation is that the different mechanisms of entropy production (at least 2: irreversibility of isotherms and adiabatics) lead to an optimal distribution of irreversible transformation times in finite time, even for energy optimization.
In addition, the introduction of the concept of entropic action has allowed us to show that, in the presence of a finite constraint of entropic actions, energy optimization occurs at the equipartition of entropic actions of the 4 transformations of the cycle. This result should be compared with other previously discovered results including reference [14].
We will now consider the power of the thermomechanical engine.
3 Power optimization of an endo-irréversible Carnot engine
It should be noted here that, without distinguishing them, the literature reveals two formally different approaches. Thus the first works [6,8] concerned systems in steady state or permanent dynamic conditions in the sense of the fluid mechanics, in which time does not occur explicitly. Thus many publications, developing the hypothesis of a stationary dynamic regime, are not explicitly related to the Thermodynamics in Finite Time (TTF).
The second approach corresponds to that of Section 2 and focuses on a cycle of period ζ, approach similar to that of Curzon and Ahlborn [4], but completed as it will be illustrated below.
3.1 Synthesis of energy optimization
We recall here the essential result obtained in Section 2:
in Irreversible Thermodynamics the MAX W of converted energy is obtained, at the minimum of entropy production ΔSI. Thus if TCS = T0, the ambient temperature, we obtain the theorem of GOUY-STODOLA [15,16]. We renew that converted energy is more general than mechanical energy as what the case at the time of Carnot.
On the other hand, this energy optimization concerns only one cycle, and not the behaviour of a system in transient mode. This will be the subject of future work, which has already begun [17].
3.2 Power optimization
The previous synthesis is taken as the starting point for the optimization in average power over a cycle 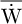 (W) (and not the instantaneous power). This average power is a function of ζ, the cycle period, obtained from (23) in the form:
(W) (and not the instantaneous power). This average power is a function of ζ, the cycle period, obtained from (23) in the form:
It is easy to see that this power is cancelled for ζ tending towards infinity (Equilibrium. Thermodynamics), but also for ζlim, limiting period such that: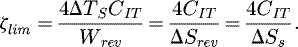 (25)
(25)
Between these two values, there is a period ζ* (or a frequency x*) leading to the maximum power: (26)
(26)
This period is proportional to the total entropic action coefficient CIT and inversely proportional to the heat transfer entropy available at the hot source under reversibility conditions. Hence the maximum average power: (27)
(27)
 (28)
(28)
The efficiency associated with this  is:
is: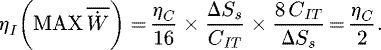 (29)
(29)
We therefore confirm a result that appears repeatedly in some works. The average maximum power output differs from the one presented by Curzon-Ahlborn. It is, according to us, more general since resulting from a triple sequential optimization of the Carnot endo-irreversible engine (energy optimisation in relation to ζi; optimization in relation to the coefficients of action for the production of entropy of the transformations CIi; average power optimization with respect to ζ cycle period).
4 Discussion − synthesis of results
This note, unlike most of the existing works, considers a thermomechanical engine model of exo-reversible and endo-irreversible Carnot cycle, while endo-reversibility is rather developed. In addition, if thermal losses are considered, it has been shown that the efficiency in the sense of the first law of thermodynamics depends on 2 ratios having as reference the heat transfer entropy available at the source under reversibility conditions:
-
dI, the degree of irreversibility of the converter.
-
dLS, the degree of thermal loss of the system including source and sink. This ratio characterizes the system's non-adiabaticity.
In the case of the endo-irreversible Carnot engine without thermal losses while retaining the same entropic reference, it has been shown that there is a first optimum of mechanized ( and more) energy related to the durations of isothermal and adiabatic transformations. This is to put in parallel to results reported in [14]. To do this, we introduced the new concept of entropic action for each transformation. We obtained an expression of the maximum energy depending on the duration of the cycle and the entropy production actions of each transformation.
A second optimization of the mechanized energy which presupposes the actions of production of entropy finished and bounded by a total entropy production action CIT, leads to an optimal distribution with equipartition of the entropy production actions of each transformation.
The average power optimization of the endo-irreversible Carnot engine was then conducted in relation to the duration of the cycle. The optimum of this power is obtained for a period that is:
The optimal period is therefore related to the ratio of the total entropy production action of the cycle divided by the heat transfer entropy available in the reversible case at the heat source. The efficiency associated with the average maximum power is then half the Carnot efficiency, generally confirming a result that appears in some works. The result differs fundamentally from the one obtained by Curzon and Ahlborn in the endo-reversible case.
Extensions of this proposal arein progress. They follow communications made in 2019 at two international conferences (JETC19, ECOS19).
This article was initially written in French in tribute to S. Carnot, one of the fathers of thermodynamics, and probably the most cited French scientist in the world thanks to his opuscule [2], unique work of his short life.
Author contribution statement
M. Feidt realized the modeling. The results were discussed jointly by the two authors. The form of the paper was organized by R. Feidt. Improvements and comments to reviewers are done in common. - Full names of conferences (JETC19, ECOS19): JETC19, ECOS10 (not only acronyms). Joint european thermodynamics conference, Barcelona Spain, 21–24 May 2019. 32d International conference on efficiency, cost, optimization, simulation and environmental impact of energy systems, Wroclaw Poland, 23–28 June 2019.
References
- L. Carnot, Principes fondamentaux de l'équilibre et du mouvement, Paris (1803) [Google Scholar]
- S. Carnot, Réflexion sur la puissance motrice du feu, Paris, Bachelier (1824) [Google Scholar]
- V.M. Brodiansky, Sadi Carnot 1796–1832, collection Etudes, Presses Universitaires de Perpignan (2006) [Google Scholar]
- F. Curzon, B. Ahlborn, Am. J. Physiol. 43 , 22 (1975) [Google Scholar]
- M. Feidt, Entropy 19 , 369 (2017) [Google Scholar]
- P. Chambadal, Les centrales nucléaires (Armand Colin, Paris, France, 1957) [Google Scholar]
- I. Novikov, At. Energ. 3 , 409 (1957) [Google Scholar]
- L. Ser, in Traité de physique industrielle: production et utilisation de la chaleur, pp. 848–852 (source gallica.bnf.fr) (1888–1892) [Google Scholar]
- M. Feidt, M. Costea, S. Petrescu, C. Stanciu, Entropy 18 , 243 (2016) [Google Scholar]
- M. Blaise, M. Feidt, D. Maillet, Energy Convers. Manage. 163 , 444 (2018) [Google Scholar]
- J. Gonzales-Ayala, J.M. Roco, A. Medina, A. Calvo-Hernandez, Entropy 19 , 182 (2017) [Google Scholar]
- J. Wang, J. He, Phys. Rev. E 86 , 051112 (2012) [Google Scholar]
- R. Esposito, R. Kawai, K. Lindenberg, C. Vandenbroeck, Phys. Rev. Lett. 105 , 150603 (2010) [Google Scholar]
- D Tondeur, Optimisation thermodynamique, Equipartition de production d'entropie, chapitres BE8017, BE 8018 (15 pages, 19 pages), Techniques de l'ingénieur (2013) [Google Scholar]
- I. Lucia, AAPP 94 , 1 (2016) [Google Scholar]
- M. Gouy, Journal de Physique. 94 , 501 (1889) [Google Scholar]
- M Feidt, in Finite Physical Dimension Optimal Thermodynamics, 1 Fundamentals (chapter 6, ISTE-ELSEVIER, 2017), pp. 189–191 [Google Scholar]
Cite this article as: Michel Feidt, Renaud Feidt, Endo-irreversible thermo-mechanical Carnot engine with new concept of entropy production action coefficient, Eur. Phys. J. Appl. Phys. 94, 30901 (2021)
All Figures
 |
Fig. 1 General schematic representation of the endo-irreversible Carnot engine with thermal losses. |
| In the text | |
 |
Fig. 2 Representation of the reversible and endo-irreversible Carnot cycles, in the diagram (T, S). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.